题目内容

已知函数f（x）=
ax-6
x2+b
的图象在点M（-1，f（-1））处的切线方程为x+2y+5=0，则a+b=（　　）
A、3B、2C、5D、4
考点：利用导数研究曲线上某点切线方程
专题：导数的概念及应用
分析：求函数的导数，根据导数的几何意义结合切线方程即可得到结论．
解答： 解：∵函数f（x）=
ax-6
x2+b
的图象在点M（-1，f（-1））处的切线方程为x+2y+5=0，
∴切线斜率k=-
1
2
，且f（-1）=-2，
则f′（x）=
a(x2+b)-2x(ax-6)
(x2+b)2
=
-ax2+ab+12x
(x2+b)2
，
则f′（-1）=
-a+ab-12
(1+b)2
=-
1
2
，且
-a-6
1+b
=-2，
两式联立解得a=2，b=3，即a+b=5，
故选：C
点评：本题主要考查导数的计算，根据导数的几何意义建立方程关系是解决本题的关键．
练习册系列答案
相关题目
在四棱锥P-ABCD中，∠ABC═∠ACD=90°，∠BAC=∠CAD=60°，PA⊥底面ABCD，E为PD的中点，PA=2AB=2．
（1）求四棱锥P-ABCD的体积V；
（2）求二面角E-AC-D的大小．
设函数f（x）=
1
2
x2-（4+a）x+6ln（x+b），g（x）=5ln（x+b）+
1
2
x2-3x，函数f（x）在x=1与x=2处取得极值．
（1）求实数a、b的值；
（2）若φ（x）=f（x）-g（x），求证：当x∈（-1，+∞）时，φ（x）≤0恒成立；
（3）证明：若x＞0，y＞0，则xlnx+ylny≥（x+y）ln
x+y
2
．
已知函数f（x）=
1
4
x4-
1
2
ax3+4x-3（a＞0）．
（Ⅰ）若f（x）在x=1处切线与直线x+2y-3=0垂直，求a的值；
（Ⅱ）若f（x）在[0，+∞）为增函数，求a的取值范围．
与曲线
x2
24
+
y2
49
=1共焦点，而与曲线
x2
36
-
y2
64
=1共渐近线的双曲线方程为（　　）
A、
y2
16
-
x2
9
=1
B、
x2
16
-
y2
9
=1
C、
y2
9
-
x2
16
=1
D、
x2
9
-
y2
16
=1
点M（x，y）（x，y）与定点F1（-4，0）的距离，和点到直线l：x=-
25
4
的距离的比是常数
4
5
，则点M的轨迹方程是
 
．
已知
a
、
b
、
c
是不共面的三个向量，则下列向量组能作为一个基底的是（　　）
A、2
a
，
a
-
b
，
a
+2
b
B、2
b
，
b
-
a
，
b
+2
a
C、
a
，2
b
，
b
-
c
D、
c
，
a
+
c
，
a
-
c
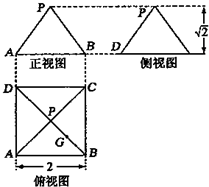某几何体的三视图如图所示，P是正方形ABCD对角线的交点，G是PB的中点．
（Ⅰ）根据三视图，画出该几何体的直观图；
（Ⅱ）在直观图中，①证明：PD∥面AGC；②证明：面PBD⊥AGC．
若
lim
x→-∞
(
x2-x+1
+x-k)=1，则k=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网