题目内容
正四面体棱长为1，其外接球的表面积为（ ）
A、
| ||
| B、π | ||
C、
| ||
| D、3π |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：由正四面体的棱长，求出正四面体的高，设外接球半径为x，利用勾股定理求出x的值，可求外接球的表面积．
解答：
解：正四面体的棱长为：1，底面三角形的高：
，
棱锥的高为：
=
，
设外接球半径为x，
x2=（
-x）2+（
）2，解得x=
，
所以外接球的表面积为：4π×（
）2=
故选：C．
| ||
| 2 |
棱锥的高为：
12-(
|
| ||
| 3 |
设外接球半径为x，
x2=（
| ||
| 3 |
| ||
| 3 |
| ||
| 4 |
所以外接球的表面积为：4π×（
| ||
| 4 |
| 3π |
| 2 |
故选：C．
点评：本题考查球的内接多面体的知识，考查计算能力，逻辑思维能力，是基础题．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
若a=ln2.7，b=ln2.8，c=e-e，则a，b，c的大小顺序是（ ）
| A、a＞b＞c |
| B、c＞b＞a |
| C、b＞c＞a |
| D、b＞a＞c |
函数f（x）=
的定义域为（ ）
| 2x-1 |
| A、（-∞，0） |
| B、（-∞，0] |
| C、（0，+∞） |
| D、[0，+∞） |
若函数y=f（x）的定义域为[-1，5]，则函数y=f（3-2x）的定义域是（ ）
A、[-
| ||
| B、[-1，2] | ||
| C、[-1，5] | ||
D、[
|
在四棱锥P-ABCD中，∠ABC═∠ACD=90°，∠BAC=∠CAD=60°，PA⊥底面ABCD，E为PD的中点，PA=2AB=2．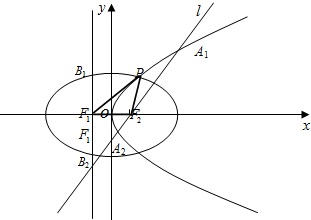
如图，设抛物线C1：y2=4mx（m＞0）的准线与x轴交于F1，焦点为F2；以F1、F2为焦点，离心率e=