题目内容
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,椭圆
,椭圆![]() 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且线段
,且线段![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() ,求点
,求点![]() 横坐标的取值范围.
横坐标的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设椭圆![]() 的标准方程为:
的标准方程为:![]() ,根据离心率为
,根据离心率为![]() ,椭圆
,椭圆![]() 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为![]() ,可得
,可得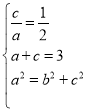 ,即可求得答案;
,即可求得答案;
(2)设![]() 的中点为
的中点为![]() ,直线
,直线![]() 联立椭圆
联立椭圆![]() 和直线
和直线![]() 方程:
方程: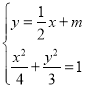 ,解得
,解得![]() 范围,根据点差法求得
范围,根据点差法求得![]() 与
与![]() 关系式,结合已知条件,即可求得答案.
关系式,结合已知条件,即可求得答案.
(1)设椭圆![]() 的标准方程为:
的标准方程为:![]()
![]() 离心率为
离心率为![]() ,椭圆
,椭圆![]() 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为![]() .
.
![]()
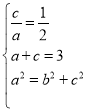 解得:
解得: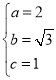
![]() 椭圆
椭圆![]() 的标准方程为:
的标准方程为:![]()
(2)设![]() 的中点为
的中点为![]() ,直线
,直线![]()
联立椭圆![]() 和直线
和直线![]() 方程:
方程: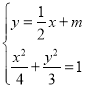 ,消掉
,消掉![]()
解得:![]()
![]() 直线
直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]()
![]()
![]() ,即:
,即:![]()
解得:![]()
设点![]() ,代入椭圆
,代入椭圆![]() 方程得:
方程得:
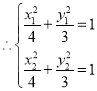
将两个方程作差可得:
![]() 即:
即:![]()
可得: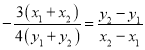
![]() ①
①
根据![]() 与
与![]() 垂直可得:
垂直可得:![]()
![]() ②
②
又![]() 根据两点
根据两点![]() 的中点为
的中点为![]() ,由中点坐标公式可得:
,由中点坐标公式可得: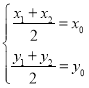
![]()
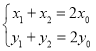
![]() ③
③
将②③代入①中可得:![]() .
.![]() ④
④
将![]() 代入直线
代入直线![]() 中得:
中得:![]()
![]() ⑤
⑤
联立④⑤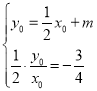 得:
得: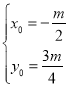
![]() 的中垂线方程为:
的中垂线方程为:![]()
当![]() ,是可得:
,是可得:
 ,
,
又![]()
![]()
![]()
![]()
![]() 点
点![]() 横坐标的取值范围:
横坐标的取值范围:![]() .
.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目