题目内容
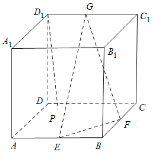
【题目】如图，在棱长为2的正方体
中，
分别为
的中点，点
在平面
内，若直线
与平面
没有公共点，则线段长的最小值是( )
A.
B.
C.
D.
【答案】D
【解析】
方法一：连接
，可证得平面
平面
，根据题意得到点
在直线
上，再根据图形的特点得当为中点时，线段
的长度最小，于是可得所求．
方法二：连接
，可得直线
平面．延长
，与
的延长线交于点
，连接
，则
，所以点在直线上，结合图形得当为中点时，线段的长度最小，进而可得答案．
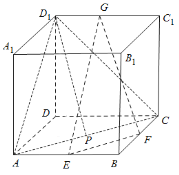
解法一：如图，连接，
由
分别为
的中点可得
，
所以
平面
．
同理可得
平面，
所以可得平面平面．
因为与平面没有公共点，
所以直线平面，
所以点在直线上，
所以当为中点时，线段的长度最小，此时
．
故选D．
解法二：如图，连接，
因为直线与平面没有公共点，
所以直线平面．
延长，与的延长线交于点，连接，
则，
所以点在直线上，
易得当为中点时，线段的长度最小，此时．
故选D．
练习册系列答案
全能练考卷系列答案
相关题目
【题目】在抽取彩票“双色球”中奖号码时，有33个红色球，每个球的编号分别为01，02，…，33.一位彩民用随机数表法选取6个号码作为6个红色球的编号，选取方法是从下面的随机数表中第1行第6列的数字3开始，从左向右读数，则依次选出的第3个红色球的编号为（ ）
49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 |
57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
A.21B.32C.09D.20
