题目内容
设f(x)是定义在R上的偶函数满足,f(x)=f(x+2),已知x∈(0,1)时,f(x)=2x-1,则f(log
6)的值为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
考点:函数的周期性,对数的运算性质
专题:函数的性质及应用
分析:本题利用函数的奇偶性和周期性,将自变量log
6转化为log 2
,利用条件x∈(0,1)时,f(x)=2x-1求出函数值f(log 2
),得到f(log
6)的值,即本题结论.
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
解答:
解:∵函数f(x)是定义在R上的偶函数,
∴f(-x)=f(x).
∵f(x)=f(x+2),
∴f(log
6)=f(log2
)=f(-log26)=f(log26)=f(log26-2)=f(log 2
).
∵当x∈(0,1)时,f(x)=2x-1,log 2
∈(0,1),
∴f(log 2
)=2 log2
-1=
-1=
.
∴f(log
6)=
.
故选B.
∴f(-x)=f(x).
∵f(x)=f(x+2),
∴f(log
| 1 |
| 2 |
| 1 |
| 6 |
| 3 |
| 2 |
∵当x∈(0,1)时,f(x)=2x-1,log 2
| 3 |
| 2 |
∴f(log 2
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴f(log
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题考查了函数的周期性、奇偶性的应用,本题难度不大,属于基础题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
若函数f(x)=-sin2ωx-6sinωxcosωx+3cos2ωx(ω>0)的最小正周期为2π,若对任意x∈R都有f(x)-1≤|f(α)-1|,则tanα的值为( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
以茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( )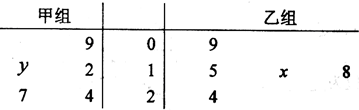

| A、5,2 | B、5,5 |
| C、8,5 | D、8,8 |
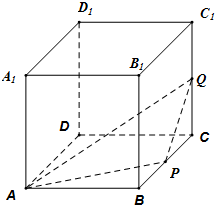 正方体ABCD-A1B1C1D1为棱长为1,动点P,Q分别在棱BC,CC1上,过点A,P,Q的平面截该正方体所得的截面记为S,设BP=x,CQ=y,其中x,y∈[0,1],下列命题正确的是
正方体ABCD-A1B1C1D1为棱长为1,动点P,Q分别在棱BC,CC1上,过点A,P,Q的平面截该正方体所得的截面记为S,设BP=x,CQ=y,其中x,y∈[0,1],下列命题正确的是