题目内容

已知椭圆C：
x2
25
+
y2
9
=1的右焦点为F，过F作与坐标轴不垂直的直线l，交椭圆于A、B两点，线段AB的中垂线l′交x轴于点M．
（1）若BF=2，求B点坐标；
（2）问：
AB
FM
是否为定值．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）设B（x1，y1），由椭圆的第二定义得：
2
25
4
-x1
=
4
5
，由此能求出B点坐标．
（2）设直线l的方程为y=k（x-4），不妨取B（
15
4
，
3
7
4
），得直线l的方程为y=-3
7
（x-4），联立
y=-3
7
(x-4)
x2
25
+
y2
9
=1
，得176x2-1400x+2775=0，解得A（
185
44
，-
27
7
44
），B（
15
4
，
3
7
4
），由此能求出
AB
FM
为定值
5
2
．
解答： 解：（1）∵椭圆C：
x2
25
+
y2
9
=1的右焦点为F，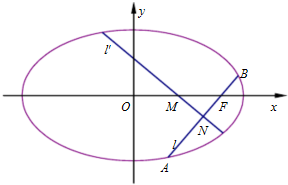
过F作与坐标轴不垂直的直线l，交椭圆于A、B两点，
BF=2，设B（x1，y1）
∴由椭圆的第二定义得：
2
25
4
-x1
=
4
5
，
解得x1=
15
4
，
∵B（x1，y1）在椭圆C：
x2
25
+
y2
9
=1上，
∴
(
15
4
)2
25
+
y12
9
=1，解得y1=±
3
7
4
，
∴B（
15
4
，-
3
7
4
）或B（
15
4
，
3
7
4
）．
（2）设直线l的方程为y=k（x-4），不妨取B（
15
4
，
3
7
4
），
把B（
15
4
，
3
7
4
）代入直线y=k（x-4），得k=-3
7
，
∴直线l的方程为y=-3
7
（x-4），
联立
y=-3
7
(x-4)
x2
25
+
y2
9
=1
，得176x2-1400x+2775=0，
解得A（
185
44
，-
27
7
44
），B（
15
4
，
3
7
4
），
∴AB=
(
185
44
-
15
4
)2+(-
27
7
44
-
3
7
4
)2
=
40
11
，
AB的中点N（
175
44
，
3
7
44
），kl′=
1
3
7
，
∴直线l′的方程为y-
3
7
44
=
1
3
7
(x-
175
44
)，
令y=0，得M（
28
11
，0），
∴MF=|4-
28
11
|=
16
11
，
∴
AB
FM
=
40
11
16
11
=
5
2
，
故
AB
FM
为定值
5
2
．
点评：本题考查点的坐标的求法，考查两线段的比值为定值的求法，解题时要认真审题，注意函数与方程思想的合理运用．
练习册系列答案
相关题目
在△ABC中，a、b、c是三个内角A、B、C对应的三边，已知b2+c2=a2+bc．
（1）求角A的大小；
（2）若sinB sinC=
3
4
，试判断△ABC的形状，并说明理由．
为了调查教师对党的群众路线学习情况，教委拟采用分层抽样的方法从甲乙丙三所不同的中学抽取90名教师进行调查．已知甲乙丙校中分别有180，270，90名教师，则从C学校中应抽取的人数为（　　）
A、10B、60C、15D、24
已知函数f（x）=（2x-x2）ex，则（　　）
A、f(
2
)是f（x）的极大值也是最大值
B、f(
2
)是f（x）的极大值但不是最大值
C、f(-
2
)是f（x）的极小值也是最小值
D、f（x）没有最大值也没有最小值
下列说法错误的是（　　）
A、已知命题p为“?x∈[0，+∞），（log32）x≤1”，则￢p是真命题
B、若p∨q为假命题，则p、q均为假命题
C、x＞2是x＞1充分不必要条件
D、“全等三角形的面积相等”的否命题是假命题
设函数f（x）=x3-2ex2+mx-lnx，记g（x）=
f(x)
x
，若函数g（x）至少存在一个零点，则实数m的取值范围是（　　）
A、（-∞，e2+
1
e
]
B、（0，e2+
1
e
]
C、（e2+
1
e
，+∞]
D、（-e2-
1
e
，e2+
1
e
]
正方体ABCD-A1B1C1D1为棱长为1，动点P，Q分别在棱BC，CC1上，过点A，P，Q的平面截该正方体所得的截面记为S，设BP=x，CQ=y，其中x，y∈[0，1]，下列命题正确的是
 
．（写出所有正确命题的编号）
①当x=0时，S为矩形，其面积最大为1；
②当x=y=
1
2
时，S为等腰梯形；
③当x=
1
2
，y∈（
1
2
，1）时，设S与棱C1D1的交点为R，则RD1=2-
1
y
；
④当y=1时，以B1为顶点，S为底面的棱锥的体积为定值
1
3
．
用三段论证明：在梯形ABCD中，如果AD∥BC，AB=CD，则∠B=∠C．
函数y=tan|x|的单调区间为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网