题目内容
11.已知点F1,F2为双曲线C:x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左、右焦点,过F2作垂直于x轴的直线,在x轴上方交双曲线于点M,且∠MF1F2=30°,圆O的方程为x2+y2=b2.(1)求双曲线C的方程;
(2)过圆O上任意一点Q(x0,y0)作切线l交双曲线C于A,B两个不同点,AB中点为N,求证|$\overrightarrow{AB}$|=2|$\overrightarrow{ON}$|.
分析 (1)确定|MF2|=b2,|MF1|=2b2,由双曲线的定义可知:|MF1|-|MF2|=b2=2,从而可得双曲线C的方程;
(2)分类讨论:①当切线l的斜率存在,设切线l的方程代入双曲线C中,利用韦达定理,结合直线l与圆O相切,可得|AB|=2|ON|成立;②当切线l的斜率不存在时,求出A,B的坐标,即可得到结论.
解答 (1)解:设F2,M的坐标分别为($\sqrt{1+{b}^{2}}$,0),($\sqrt{1+{b}^{2}}$,y0)
因为点M在双曲线C上,所以1+b2-$\frac{{{y}_{0}}^{2}}{{b}^{2}}$=1,即y0=±b2,所以|MF2|=b2,
在Rt△MF2F1中,∠MF1F2=30°,|MF2|=b2,所以|MF1|=2b2…(2分)
由双曲线的定义可知:|MF1|-|MF2|=b2=2
故双曲线C的方程为:${x}^{2}-\frac{{y}^{2}}{2}=1$…(4分)
(2)证明:由题意,即证:OA⊥OB.
设A(x1,y1),B(x2,y2),切线l的方程为:x0x+y0y=2…(11分)
①当y0≠0时,切线l的方程代入双曲线C中,化简得:(2y02-x02)x2+4x0x-(2y02+4)=0
所以:x1+x2=-$\frac{4{x}_{0}}{2{{y}_{0}}^{2}-{{x}_{0}}^{2}}$,x1x2=-$\frac{2{{y}_{0}}^{2}+4}{2{{y}_{0}}^{2}-{{x}_{0}}^{2}}$
又y1y2=$\frac{8-2{{x}_{0}}^{2}}{2{{y}_{0}}^{2}-{{x}_{0}}^{2}}$…(13分)
所以$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=-$\frac{2{{y}_{0}}^{2}+4}{2{{y}_{0}}^{2}-{{x}_{0}}^{2}}$+$\frac{8-2{{x}_{0}}^{2}}{2{{y}_{0}}^{2}-{{x}_{0}}^{2}}$=0…(15分)
②当y0=0时,易知上述结论也成立.
所以$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=0…(16分)
综上,OA⊥OB,所以|$\overrightarrow{AB}$|=2|$\overrightarrow{ON}$|.
点评 本题考查双曲线的标准方程,考查直线与双曲线的位置关系,考查韦达定理的运用,考查向量知识,考查学生的计算能力,属于中档题.

| A. | (-∞,1] | B. | (-∞,0)∪(0,1) | C. | (-∞,0)∪(0,1] | D. | [1,+∞) |
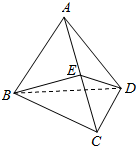 如图,平面ABC⊥平面BCD,AB=BC=BD=2,∠ABC=∠DBC=$\frac{π}{3}$,E为棱AD的中点.
如图,平面ABC⊥平面BCD,AB=BC=BD=2,∠ABC=∠DBC=$\frac{π}{3}$,E为棱AD的中点.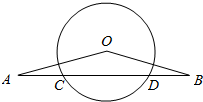 已知:如图△OAB为等腰三角形,底边AB角⊙O于点C,D,求证:AC=BD.
已知:如图△OAB为等腰三角形,底边AB角⊙O于点C,D,求证:AC=BD.