��Ŀ����
����Ŀ��2017�ꡰʮһ���ڼ䣬���ٹ�·�����϶࣮ij���鹫˾��һ����������������С�������а������������Ⱥ�ÿ���50���ͳ�ȡһ���ij���������ȡ40����ʻԱ����ѯ�ʵ��飬��������ij�θ��ٹ�·�ij��٣�![]() ���ֳ����Σ�
���ֳ����Σ� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
����õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
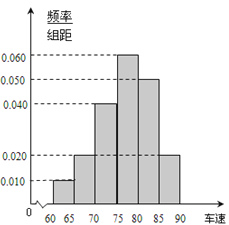
��1������40��С�ͳ������ٵ���������λ���Ĺ���ֵ��
��2�����ӳ�����![]() �ij������γ�ȡ2����������
�ij������γ�ȡ2����������![]() �ij���ǡ��һ���ĸ��ʣ�
�ij���ǡ��һ���ĸ��ʣ�
���𰸡���1��77.5�� ![]() ����2��
����2��![]() ��
��
���������������; ��1��ѡ��ֱ��ͼ����ߵľ��������ױߵ��е㼴Ϊ�������������߿�ʼС���ε������Ϊ0.5��Ӧ�ĺ�������Ϊ��λ�������ø���С���ε�������Զ�Ӧ���εĵױߵ��е�ĺ�Ϊ���ݵ�ƽ������
��2����ͼ�п�֪��������![]() �ij������ͳ�����
�ij������ͳ�����![]() �ij��������ӳ�����
�ij��������ӳ�����![]() �ij������γ�ȡ2�����賵����
�ij������γ�ȡ2�����賵����![]() �ij�����Ϊ
�ij�����Ϊ![]() ������
������![]() �ij�����Ϊ
�ij�����Ϊ![]() �г����ԵĻ����¼������Ӷ������Ӧ�ĸ��ʼ��ɣ�
�г����ԵĻ����¼������Ӷ������Ӧ�ĸ��ʼ��ɣ�
���������
��1�������Ĺ���ֵΪ��ߵľ��ε��е㣬�������Ĺ���ֵ����77.5��
��ͼ����������Ӧ�ij���Ϊ![]() ������λ���Ĺ���ֵΪ��
������λ���Ĺ���ֵΪ��
![]() �����
�����![]() ��
��
����λ���Ĺ���ֵΪ![]() ��
��
��2����ͼ�п�֪��������![]() �ij�����Ϊ��
�ij������� ![]() ��������
��������
������![]() �ij�������
�ij������� ![]() ��������
��������
�賵����![]() �ij�����Ϊ
�ij�����Ϊ![]() ��
�� ![]() ��������
��������![]() �ij�����Ϊ
�ij�����Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �������л����¼��У�
�������л����¼��У�
![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��15�֣�
��15�֣�
���г�����![]() �ij���ǡ��һ�����¼��У�
�ij���ǡ��һ�����¼��У� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��8�֣�
��8�֣�
���ԣ�������![]() �ij���ǡ��һ���ĸ���Ϊ
�ij���ǡ��һ���ĸ���Ϊ![]() ��
��
