题目内容
设数列{an}满足:an+1an=2an+1-2(n=1,2,…),a2009=,则此数列的前2009项的和为 .
2008+.
:若an+1≠0,则an=2-,故a2008=2-,a2007=2-=-,a2006=2+,a2005=.一般的,若an≠0,1,2,则an=2-,则an-1=,an-2=,an-3=an+1,故an-4=an.
于是,Σk=1an=502(a1+a2+a3+a4)+a2009=502(a2005+a2006+a2007+a2008)+a2009=2008+.
于是,Σk=1an=502(a1+a2+a3+a4)+a2009=502(a2005+a2006+a2007+a2008)+a2009=2008+.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 的两个实根,数列
的两个实根,数列 满足
满足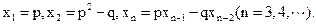

 求
求 。
。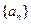 中,
中,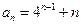 ,
, .
. 项和
项和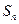 ;(2)证明不等式
;(2)证明不等式 ,对任意
,对任意 +
+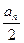 (n∈N+),则其{an}的前10项和为
(n∈N+),则其{an}的前10项和为 的前
的前 项和
项和 .
.