题目内容
设e1,e2是平面内两个互相垂直的单位向量,若向量m满足(m-e1)·(m-e2)=0,则|m|的最大值为( )
| A.1 | B.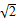 | C.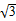 | D.2 |
B
因为|e1|=|e2|=1,e1⊥e2,
所以(m-e1)·(m-e2)
=m2-m·(e1+e2)+e1·e2
=m2-m·(e1+e2)=0,
即m2=m·(e1+e2).
设m与e1+e2的夹角为θ,
因为|e1+e2|=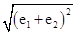
=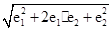 =
=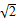 ,
,
所以|m|2=|m||e1+e2|cosθ,
即|m|=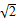 cosθ,因为θ∈[0,π],
cosθ,因为θ∈[0,π],
所以|m|max=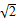 .
.
所以(m-e1)·(m-e2)
=m2-m·(e1+e2)+e1·e2
=m2-m·(e1+e2)=0,
即m2=m·(e1+e2).
设m与e1+e2的夹角为θ,
因为|e1+e2|=
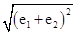
=
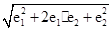 =
=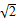 ,
,所以|m|2=|m||e1+e2|cosθ,
即|m|=
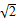 cosθ,因为θ∈[0,π],
cosθ,因为θ∈[0,π],所以|m|max=
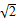 .
.
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
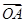 +
+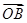 +2
+2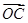 =0,则△ABC的面积与△AOC的面积的比值为( )
=0,则△ABC的面积与△AOC的面积的比值为( )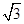
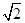
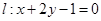 与⊙C:
与⊙C: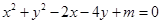 (
(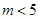 )
)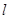 与⊙C相交,求
与⊙C相交,求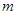 的取值范围。
的取值范围。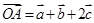 ,
,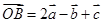 ,
,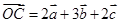 ,
,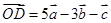 ,其中
,其中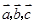 三向量不共面.试判断A,B,C,D四点是否共面?
三向量不共面.试判断A,B,C,D四点是否共面?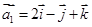 ,
,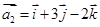 ,
,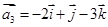 ,
,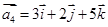 .试问是否存在实数
.试问是否存在实数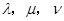 ,使
,使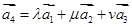 成立?如果存在,求出
成立?如果存在,求出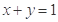 与圆
与圆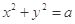 交于
交于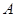 、
、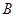 两点,
两点,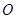 是原点,C是圆上一点,若
是原点,C是圆上一点,若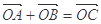 ,则
,则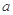 的值为_______ .
的值为_______ .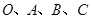 ,若
,若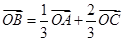 ,则
,则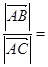 .
.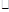 b=-6,则向量el与e2的夹角是
b=-6,则向量el与e2的夹角是



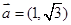 ,
,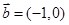 ,则
,则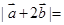 ( )
( )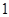
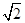
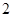
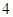
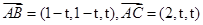 ,则
,则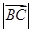 的最小值为
的最小值为