题目内容
数列{an}的前n项和为Sn,a1=2,Sn=
an+1-1(n∈N*).
(Ⅰ)求a2,a3;
(Ⅱ)求数列{an}的通项an;
(Ⅲ)求数列{nan}的前n项和Tn.
| 1 |
| 2 |
(Ⅰ)求a2,a3;
(Ⅱ)求数列{an}的通项an;
(Ⅲ)求数列{nan}的前n项和Tn.
(Ⅰ)∵a1=2,Sn=
an+1-1(n∈N*),
∴当n=1时,S1=
a2-1=a1=2,
解得a2=6.
当n=2时,S2=
a3-1=2+6=8,
解得a3=18.
(Ⅱ)∵a1=2,Sn=
an+1-1(n∈N*),
∴当n≥2时,Sn=
an+1-1,Sn-1=
an-1,
∴an=Sn-Sn-1=
an+1-
an,
即an+1=3an.
对于a2=3a1也满足上式,
∴数列{an}是首项为2,公比为3的等比数列,
∴an=2•3n-1(n∈N*).
( III)∵an=2•3n-1(n∈N*),
∴nan=2n•3n-1,
∴Tn=2•1+4•3+6•32+8•33+…+2n•3n-1,
3Tn=2•3+4•32+6•33+8•34+…+2n•3n,
相减得,-2Tn=2(1+3+32+33+…+3n-1)-2n•3n
=2•
-2n•3n
=3n-1-2n•3n,
∴Tn=
.
| 1 |
| 2 |
∴当n=1时,S1=
| 1 |
| 2 |
解得a2=6.
当n=2时,S2=
| 1 |
| 2 |
解得a3=18.
(Ⅱ)∵a1=2,Sn=
| 1 |
| 2 |
∴当n≥2时,Sn=
| 1 |
| 2 |
| 1 |
| 2 |
∴an=Sn-Sn-1=
| 1 |
| 2 |
| 1 |
| 2 |
即an+1=3an.
对于a2=3a1也满足上式,
∴数列{an}是首项为2,公比为3的等比数列,
∴an=2•3n-1(n∈N*).
( III)∵an=2•3n-1(n∈N*),
∴nan=2n•3n-1,
∴Tn=2•1+4•3+6•32+8•33+…+2n•3n-1,
3Tn=2•3+4•32+6•33+8•34+…+2n•3n,
相减得,-2Tn=2(1+3+32+33+…+3n-1)-2n•3n
=2•
| 1-3n |
| 1-3 |
=3n-1-2n•3n,
∴Tn=
| (2n-1)•3n+1 |
| 2 |

练习册系列答案
相关题目
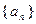 的首项
的首项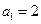 ,公比
,公比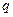 是最小的正整数,则数列
是最小的正整数,则数列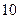 项的和为
项的和为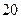 B
B 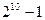 C
C 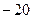 D
D