题目内容
【题目】过抛物线
）的焦点F且斜率为
的直线交抛物线C于M，N两点，且
．
（1）求p的值；
（2）抛物线C上一点
，直线
（其中
）与抛物线C交于A，B两个不同的点（A，B均与点Q不重合）．设直线QA，QB的斜率分别为
，
.直线l是否过定点？如果是，请求出所有定点；如果不是，请说明理由；
【答案】（1）
（2）直线
恒过定点
【解析】
（1）设直线
，与抛物线联立可得
，利用焦点弦长可构造方程求得
；（2）由（1）可得抛物线方程和
点坐标；联立直线与抛物线方程，可得
和韦达定理的形式；利用两点连线斜率公式表示出
，代入韦达定理结果可求得
，满足，从而得到直线方程，进而求得定点.
（1）由题意得：
，设直线
方程为：
代入抛物线方程得：
设
，
，解得：
（2）由（1）知：抛物线
设
，
由
得：
，则
，
即：
，解得：
当时，
，恒过定点
直线恒过定点
练习册系列答案
阅读快车系列答案
相关题目
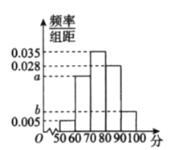
【题目】甲、乙两企业生产同一种型号零件，按规定该型号零件的质量指标值落在
内为优质品.从两个企业生产的零件中各随机抽出了
件，测量这些零件的质量指标值，得结果如下表：
甲企业：
分组 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
| 5 |
乙企业：
分组 |
|
|
|
|
|
|
|
频数 | 5 |
|
|
|
|
| 5 |
（1）已知甲企业的件零件质量指标值的样本方差
，该企业生产的零件质量指标值X服从正态分布
，其中μ近似为质量指标值的样本平均数
（注：求时，同一组中的数据用该组区间的中点值作代表），
近似为样本方差
，试根据企业的抽样数据，估计所生产的零件中，质量指标值不低于
的产品的概率.（精确到
）
（2）由以上统计数据完成下面
列联表，并判断能否在犯错误的概率不超过
的前提下认为两个企业生产的零件的质量有差异.
甲厂 | 乙厂 | 总计 | |
优质品 | |||
非优质品 | |||
总计 |
附：
参考数据：
，
参考公式：若
，则
，
，
；
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
