题目内容
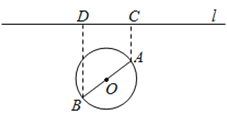
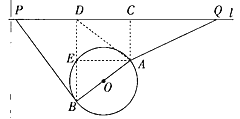
【题目】如图，一个湖的边界是圆心为
的圆，湖的一侧有一条直线型公路
，湖上有桥
（是圆的直径）.规划在公路上选两个点
，并修建两段直线型道路
.规划要求：线段上的所有点到点的距离均不小于圆的半径.已知点
到直线的距离分别为
和
（
为垂足），测得
，
，
（单位：百米）.
（1）若道路
与桥垂直，求道路的长；
（2）在规划要求下，
和
中能否有一个点选在
处？并说明理由.
【答案】（1）15（百米）；（2）不能，理由见解析
【解析】
（1）作
，可求得
，从而得到
，由
可求得结果；
（2）①若
在
处，线段
上的点（除
）到点
的距离均小于圆的半径，不符合规划要求；②若
在处，可得到
；利用余弦定理可验证出
为锐角，可知上存在点到点的距离小于圆的半径，不符合规划要求；由此可得结论.
（1）过点
作，垂足为
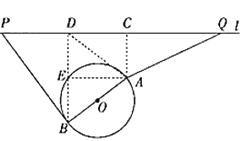
由已知条件得：四边形
为矩形 
，
道路
的长为
（百米）
（2）不能，理由如下：
①若在处，由（1）可得在圆上
则线段上的点（除）到点的距离均小于圆的半径
选在处不满足规划要求
②若在处，连接
由（1）知：
为锐角 线段上存在点到点的距离小于圆的半径
选在处也不满足规划要求
综上所述：和均不能选在处
练习册系列答案
相关题目
