题目内容
【题目】已知数列{an}的前n项和![]() .
.
(1)求数列{an}的通项公式an;
(2)设数列{bn}的前n项和为Tn,满足b1=1,![]() .
.
①求数列{bn}的通项公式bn;
②若存在p,q,k∈N*,p<q<k,使得ambq,amanbp,anbk成等差数列,求m+n的最小值.
【答案】(1) an![]() .(2) ①bn=2n﹣1;②7
.(2) ①bn=2n﹣1;②7
【解析】
(1)根据前n项和与通项的关系,即可求出通项公式;
(2)①将![]() 代入递推公式中,用裂项相消求出
代入递推公式中,用裂项相消求出![]() ,再由前n项和求出通项
,再由前n项和求出通项![]() ;
;
②由等差数列的中项性质,求出![]() 的不等量关系,结合基本不等式,即可得到
的不等量关系,结合基本不等式,即可得到![]() 最小值.
最小值.
(1)∵数列{an}的前n项和![]() .
.
∴当n=1时,a1=S1![]() ,
,
当n≥2时,an=Sn﹣Sn﹣1![]() ,
,
当![]() 时,a1
时,a1![]() ,满足上式,
,满足上式,
∴an![]() .
.
(2)①∵![]()
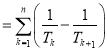
=(![]() )+(
)+(![]() )+(
)+(![]() )+…+(
)+…+(![]() )
)
![]() 1
1![]() .
.
∴1![]() ,
,
∴Tn+1=2n+1﹣1,Tn=2n﹣1,
把上面两式相减得,bn+1=2n,
∴![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 满足上式,
满足上式,
![]()
②由ambq,amanbp,anbk成等差数列,
有2amanbp=ambq+anbk,
即2![]()
![]()
![]()
![]()
![]()
![]() ,
,
由于p<q<k,且为正整数,所以q﹣p≥1,k﹣p≥2,
所以mn=m![]() +n
+n![]() ≥2m+4n,
≥2m+4n,
可得 mn≥2m+4n,![]() 1,
1,
![]()
![]() 的最小值为12,
的最小值为12,
此时![]() 或
或![]() 或
或![]() ,
,
![]() 的最小值为12.
的最小值为12.

练习册系列答案
相关题目
【题目】某仪器经过检验合格才能出厂,初检合格率为![]() :若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为
:若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为![]() .每台仪器各项费用如表:
.每台仪器各项费用如表:
项目 | 生产成本 | 检验费/次 | 调试费 | 出厂价 |
金额(元) | 1000 | 100 | 200 | 3000 |
(Ⅰ)求每台仪器能出厂的概率;
(Ⅱ)求生产一台仪器所获得的利润为1600元的概率(注:利润![]() 出厂价
出厂价![]() 生产成本
生产成本![]() 检验费
检验费![]() 调试费);
调试费);
(Ⅲ)假设每台仪器是否合格相互独立,记![]() 为生产两台仪器所获得的利润,求
为生产两台仪器所获得的利润,求![]() 的分布列和数学期望.
的分布列和数学期望.