Question

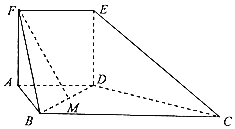
【题目】如图所示的几何体ABCDE中，平面EAB，，，，M是EC的中点．

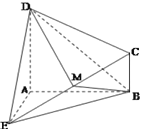
求异面直线DM与BE所成角的大小；

求二面角的余弦值．

Answer 1

【答案】（1）；（2）.

【解析】

由题意，先证明直线AE、AB、AD两两垂直，再以点A为原点，AE、AB、AD所在直线分别为x轴、y轴、z轴建立空间直角坐标系，

求出向量，然后求出异面直线DM与BE所成的角；

求出平面BDM和平面BDA的法向量，再求二面角的余弦值．

平面EAB，

平面平面EAB，

又，且平面平面，

平面ABCD，

直线AE、AB、AD两两垂直，

以点A为原点，AE、AB、AD所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系，

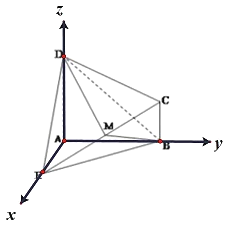
设，

0，，4，，4，，0，，0，，

是EC的中点，

2，，

，，

，

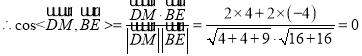异面直线DM与BE所成角的大小为；

设二面角的大小为，

，，，

设平面BDM的一个法向量,

则,且,

所以,且,

令,则,

平面BDM的一个法向量，平面BDA的一个法向量

，

由图可知，为锐角，

二面角的余弦值为．