题目内容
【题目】如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
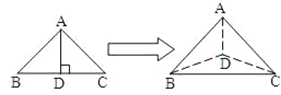
①![]() ;
;
②∠BAC=60°;
③三棱锥D﹣ABC是正三棱锥;
④平面ADC和平面ABC的垂直.
其中正确的是( )
A. ①② B. ②③ C. ③④ D. ①④
【答案】B
【解析】
①由折叠的原理,可知BD⊥平面ADC,可推知BD⊥AC,数量积为零,②因为折叠后AB=AC=BC,三角形为等边三角形,所以∠BAC=60°;③又因为DA=DB=DC,根据正三棱锥的定义判断.④平面ADC和平面ABC不垂直.
BD⊥平面ADCBD⊥AC,①错;
AB=AC=BC,②对;
DA=DB=DC,结合②,③对④错.
故选:B.

练习册系列答案
相关题目



