题目内容
16.已知正项数列{an},a1=1,an+1=an2+2an,则an=${2}^{{2}^{n-1}}$-1.分析 由已知条件推导出数列{log2(an+1)}为首项为1,公比为2的等比数列,由此能求出an.
解答 解:∵正项数列{an},a1=1,an+1=an2+2an,
∴an+1+1=an2+2an+1=(an+1)2,
∴$lo{g}_{2}({a}_{n+1}+1)=lo{g}_{2}({a}_{n}+1)^{2}$=2log2(an+1).
∴$\frac{lo{g}_{2}({a}_{n+1}+1)}{lo{g}_{2}({a}_{n}+1)}$=2,log2(a1+1)=log22=1
∴数列{log2(an+1)}为首项为1,公比为2的等比数列.
∴$lo{g}_{2}({a}_{n}+1)={2}^{n-1}$,
∴${a}_{n}+1={2}^{{2}^{n-1}}$,
∴${a}_{n}={2}^{{2}^{n-1}}-1$.
故答案为:${2}^{{2}^{n-1}}$-1.
点评 本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
相关题目
6.f(x)=x3+ax2+bx+c在区间(1,2)上有三个零点,则( )
| A. | f(1)f(2)≤$\frac{1}{64}$ | B. | f(1)f(2)<$\frac{1}{64}$ | C. | f(1)f(2)>-$\frac{1}{64}$ | D. | f(1)f(2)≥-$\frac{1}{64}$ |
4.设M={x||x|<2},N={x|x>a},全集为R,若M?$\overline{N}$,则( )
| A. | a=2 | B. | a≤2 | C. | a≥2 | D. | a<2 |
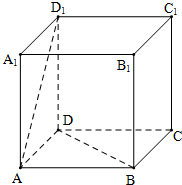 如图,正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是线段AD1和BD上的点,且D1P:PA=DQ:QB=5:12.
如图,正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是线段AD1和BD上的点,且D1P:PA=DQ:QB=5:12.