题目内容
6.f(x)=x3+ax2+bx+c在区间(1,2)上有三个零点,则( )| A. | f(1)f(2)≤$\frac{1}{64}$ | B. | f(1)f(2)<$\frac{1}{64}$ | C. | f(1)f(2)>-$\frac{1}{64}$ | D. | f(1)f(2)≥-$\frac{1}{64}$ |
分析 设f(x)=x3+ax2+bx+c在区间(1,2)上三个零点为x1,x2,x3,则f(x)=(x-x1)(x-x2)(x-x3),表示出f(1)f(2),再利用基本不等式,即可求出结论.
解答 解:设f(x)=x3+ax2+bx+c在区间(1,2)上三个零点为x1,x2,x3,则f(x)=(x-x1)(x-x2)(x-x3)
f(1)f(2)=(1-x1)(1-x2)(1-x3)(2-x1)(2-x2)(2-x3)
=-[(x1-1)(2-x1)][(x2-1)(2-x2)][(x3-1)(2-x3)]
≥-($\frac{{x}_{1}-1+2-{x}_{2}}{2}$)2•($\frac{{x}_{2}-1+2-{x}_{2}}{2}$)2•($\frac{{x}_{3}-1+2-{x}_{3}}{2}$)2=-$\frac{1}{64}$,
∵三个零点互不相等,
∴f(1)f(2)>-$\frac{1}{64}$.
故选:C.
点评 本题考查函数的零点,考查基本不等式的运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列几何体是台体的是( )
| A. | 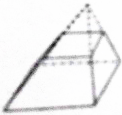 | B. | 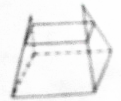 | C. |  | D. |  |
15.2013年前,我国每年浪费约500亿公斤粮食,接近全国粮食总产量的十分之一,成为了世界上最大的人为灾害.从2013年1月初开始,公众自主发起一项倡议市民厉行节约,反对浪费,在饭店就餐时适量点餐,剩餐打包,“光盘”离开的大型公益活动:“光盘行动”.为了了解活动效果,某新闻媒体对900名市民进行了网上调查,所有参与调查的市民中,持“支持”“保留”和“不支持”态度的人数如下表所示:
(Ⅰ)在持“支持”、“保留”、“不支持”态度的市民中,用分层抽样的方法抽取6个人进行电话采访,应分别抽多少人?
(Ⅱ)将(1)中抽出的6个人看成一个总体,从这6个人中任意选取3人开一个座谈会,求这3人中至少有1人持“保留”态度的概率?
| 支持 | 保留 | 不支持 |
| 450 | 300 | 150 |
(Ⅱ)将(1)中抽出的6个人看成一个总体,从这6个人中任意选取3人开一个座谈会,求这3人中至少有1人持“保留”态度的概率?
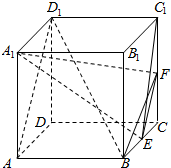 已知四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形且AA1⊥底面ABCD,AA1=4,E为BC的中点,F为CC1的中点.
已知四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形且AA1⊥底面ABCD,AA1=4,E为BC的中点,F为CC1的中点.