题目内容
4.设M={x||x|<2},N={x|x>a},全集为R,若M?$\overline{N}$,则( )| A. | a=2 | B. | a≤2 | C. | a≥2 | D. | a<2 |
分析 求出$\overline{N}$={x|x≤a},M={x||x|<2}={x|-2<x<2},利用M?$\overline{N}$,即可求得a的范围.
解答 解:∵N={x|x>a},
∴$\overline{N}$={x|x≤a},
∵M={x||x|<2}={x|-2<x<2},
∴a≥2,
故选:C.
点评 本题考查集合的包含关系,考查集合的运算,比较基础.

练习册系列答案
相关题目
14.下列几何体是台体的是( )
| A. | 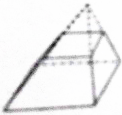 | B. | 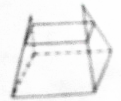 | C. |  | D. |  |
15.2013年前,我国每年浪费约500亿公斤粮食,接近全国粮食总产量的十分之一,成为了世界上最大的人为灾害.从2013年1月初开始,公众自主发起一项倡议市民厉行节约,反对浪费,在饭店就餐时适量点餐,剩餐打包,“光盘”离开的大型公益活动:“光盘行动”.为了了解活动效果,某新闻媒体对900名市民进行了网上调查,所有参与调查的市民中,持“支持”“保留”和“不支持”态度的人数如下表所示:
(Ⅰ)在持“支持”、“保留”、“不支持”态度的市民中,用分层抽样的方法抽取6个人进行电话采访,应分别抽多少人?
(Ⅱ)将(1)中抽出的6个人看成一个总体,从这6个人中任意选取3人开一个座谈会,求这3人中至少有1人持“保留”态度的概率?
| 支持 | 保留 | 不支持 |
| 450 | 300 | 150 |
(Ⅱ)将(1)中抽出的6个人看成一个总体,从这6个人中任意选取3人开一个座谈会,求这3人中至少有1人持“保留”态度的概率?
12.以椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左焦点为焦点的抛物线的标准方程是( )
| A. | y2=16x | B. | y2=-8x | C. | y2=-16x | D. | x2=-16y |
19.袋中有大小相同的红球6个,白球5个,从袋中每次任意取出1个球,直到取出的球是白球时为止,所需要的取球的次数为随机变量ξ,则ξ的可能值为( )
| A. | 1,2,…,6 | B. | 1,2,…,7 | C. | 1,2,…,11 | D. | 1,2,3… |
9.复数($\frac{i}{1+i}$)2=( )
| A. | $\frac{1}{2}$i | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$i | D. | -$\frac{1}{2}$ |