��Ŀ����
8����֪����f��x���Ķ�����ΪD��������f��x���ĵ�����f�䣨x��������������x0Ϊy=f�䣨x���ļ�ֵ�㣻��Ƶ㣨x0��f��x0�����Ǻ���f��x���Ĺյ㣮�����н�������ȷ������Ǣ٢ۣ��ٺ���y=sinx�Ĺյ�Ϊ��k�У�0����k��Z��
�ں���f��x��=ex-$\frac{1}{12}{x^4}$���ҽ��������յ㣻
��������f��x��=4xlnx+$\frac{1}{6}{x^3}+\frac{a+1}{2}{x^2}$�������յ㣬��a��-5��
�ܺ���f��x��=xex�Ĺյ�Ϊ��x0��f��x0���������
��������ʹf��x�������䣨x0-�ţ�x0�������䣨x0��x0+�ţ��ϵ��������෴��
���� ���ݹյ�Ķ��壬�õ�f�壨x0��=0����x0Ϊ�����Ĺյ㣬
���ڢ٣���������жϣ�
���ڢ��������ν�ϵ�˼�룬�õ�����ֻ��һ���յ㣬
���ڢ����ùյ�Ķ��壬���ɵõ�x2+��a+1��x+4=0�����������������a�ķ�Χ�������жϣ�
���ڢ��жϺ���f��x���ĵ����ԣ���������Ĺյ㣬�����жϣ�
���  �⣺���ڢ٣�y=sinx����y��=cosx����x0=k��ʱ�������м�ֵ�㣬f��k�У�=sin��k�У�=0��
�⣺���ڢ٣�y=sinx����y��=cosx����x0=k��ʱ�������м�ֵ�㣬f��k�У�=sin��k�У�=0��
�ʺ���y=sinx�Ĺյ�Ϊ��k�У�0����k��Z���ʢ���ȷ��
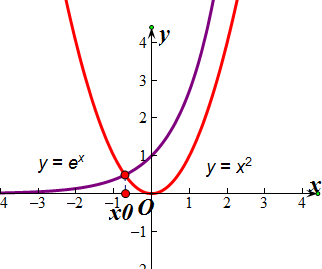
���ڢڣ�f�䣨x��=ex-$\frac{1}{3}$x3��f�壨x��=ex-x2����ͼ��ʾ��
��x=x0ʱ�����м�ֵ�㣬����ֻ��һ�����ʺ���f��x��=ex-$\frac{1}{12}{x^4}$���ҽ���һ���յ㣬�ʢڴ���
���ڢۣ�����f��x��=4xlnx+$\frac{1}{6}{x^3}+\frac{a+1}{2}{x^2}$�������յ㣬��f�䣨x��=4��1+lnx��+$\frac{1}{2}$x2+��a+1��x��
��f�壨x��=$\frac{4}{x}$+x+a+1=$\frac{{x}^{2}+��a+1��x+4}{x}$��
��f�壨x��=0����x2+��a+1��x+4=0��������������$\left\{\begin{array}{l}{��a+1��^{2}-16��0}\\{{x}_{1}+{x}_{2}=-��a+1����0}\end{array}\right.$�����a��-5��
�ʢ���ȷ��
���ڢܣ�f��x��=xex����f�䣨x��=��1+x��ex��f�壨x��=��2+x��ex��
��f�壨x��=0ʱ����x=-2������f��x���йյ㣬��յ�Ϊ��-2��-$\frac{2}{{e}^{2}}$��
��Ϊ��x��-1ʱ������f��x��������������x��-1ʱ�����������ݼ���
���Ժ����ڣ�-2-�ţ�-2���ĵ����ݼ��������䣨-2��-2+�ţ��ϵĵ�������һ�����ʢܴ���
�ʴ�Ϊ���٢ۣ�
���� ��С�⿼���¶��壬���麯���뵼����֪ʶ�����黯����ת������ѧ˼�뷽����������������������е��⣮

 ��У����ϵ�д�
��У����ϵ�д�| A�� | 1��2������6 | B�� | 1��2������7 | C�� | 1��2������11 | D�� | 1��2��3�� |
| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | 2 | D�� | $\sqrt{6}$ |
| A�� | 4 | B�� | $\frac{112}{27}$ | C�� | 4��$\frac{112}{27}$ | D�� | $\frac{112}{9}$ |