题目内容
已知等差数列 的前
的前 项和为
项和为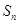 ,且
,且 .
.
(I)求数列 的通项公式;
的通项公式;
(II)设等比数列 ,若
,若 ,求数列
,求数列 的前
的前 项和
项和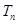
(Ⅲ)设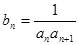 ,求数列
,求数列 的前
的前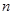 项和
项和
 的前
的前 项和为
项和为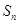 ,且
,且 .
.(I)求数列
 的通项公式;
的通项公式;(II)设等比数列
 ,若
,若 ,求数列
,求数列 的前
的前 项和
项和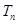
(Ⅲ)设
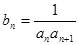 ,求数列
,求数列 的前
的前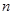 项和
项和
(Ⅰ) ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)
;(Ⅲ)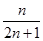 .
.
 ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)
;(Ⅲ)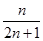 .
.试题分析:(Ⅰ)两种思路,一是根据等差数列的通项公式、求和公式,建立
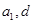 的方程组;
的方程组;二是利用等差数列的性质,由
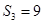 ,得
,得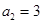 ,
,结合
 ,确定
,确定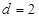 .
.(Ⅱ)由(I得
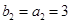 ,
, ,得到公比
,得到公比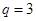 ,
,  ,应用等比数列的求和公式计算.
,应用等比数列的求和公式计算. (Ⅲ)由(Ⅰ)知,
 . 从而得到
. 从而得到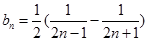 ,应用“裂项相消法”求和.
,应用“裂项相消法”求和.该题综合考查等差数列、等比数列的基础知识,以及数列求和的方法,较为典型.
试题解析:(Ⅰ)法一:
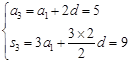 解得
解得 (2分)
(2分)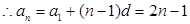 (4分)
(4分)法二:由
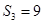 ,得
,得 ,所以
,所以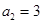 . (2分)
. (2分)又因为
 ,所以公差
,所以公差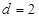 . (3分)
. (3分)从而
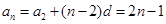 . (4分)
. (4分)(Ⅱ)由上可得
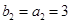 ,
, ,所以公比
,所以公比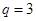 ,
, 从而,
 (6分)
(6分)所以.
 (8分)
(8分)(Ⅲ)由(Ⅰ)知,
 .
. ∴
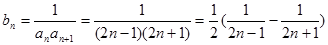 10分
10分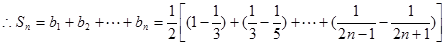
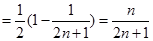 (12分)
(12分)
练习册系列答案
相关题目
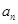 }中,a1=1,
}中,a1=1,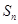 是数列{
是数列{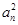 +p
+p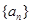 中,
中,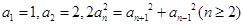 ,则
,则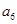 等于( )
等于( )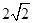
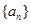 ,
,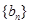 的前n项和为
的前n项和为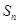 ,
,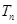 ,若对于任意的自然数
,若对于任意的自然数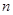 ,都有
,都有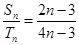 则
则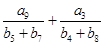 = .
= .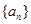 是公差不为0的等差数列,且
是公差不为0的等差数列,且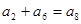 ,则
,则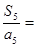 .
.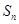 是等差数列
是等差数列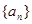 的前
的前 项和,且
项和,且 ,则
,则 的值为 .
的值为 .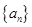 的前n项和为
的前n项和为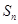 ,且
,且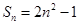 ,则
,则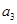 等于( )
等于( )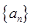 为等差数列,
为等差数列,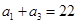 ,
, ,则
,则 .
.