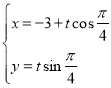题目内容
【题目】已知抛物线![]() ,过抛物线焦点
,过抛物线焦点![]() 的直线
的直线![]() 分别交抛物线
分别交抛物线![]() 和圆
和圆![]() 于点
于点![]() (自上而下).
(自上而下).
(1)求证:![]() 为定值;
为定值;
(2)若![]() 、
、![]() 、
、![]() 成等差数列,求直线
成等差数列,求直线![]() 的方程.
的方程.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)讨论当直线过焦点![]() 且垂直于
且垂直于![]() 轴时,
轴时,![]() 四点坐标可直接求出,可求得
四点坐标可直接求出,可求得![]() ,当直线过焦点
,当直线过焦点![]() 且不垂直于
且不垂直于![]() 轴时,设直线方程为
轴时,设直线方程为![]() ,联立抛物线方程,运用韦达定理和抛物线的定义,即可得到定值;
,联立抛物线方程,运用韦达定理和抛物线的定义,即可得到定值;
(1)由![]() 、
、![]() 、
、![]() 成等差数列,可得
成等差数列,可得![]() ,从而可得
,从而可得![]() ,而
,而![]() ,
,![]() ,列方程可求出斜率
,列方程可求出斜率![]() ,从而可求出直线方程.
,从而可求出直线方程.
(1)由题知,焦点![]() ,圆
,圆![]() 半径
半径![]() ;
;
①当斜率不存在时,![]() ,交点
,交点![]() ,此时
,此时![]() ;
;
②当斜率存在时,设![]() ,
,
联立![]() ,消去
,消去![]() 得
得![]()
由韦达定理得![]() ,显然
,显然![]() 恒成立
恒成立
由抛物线定义得![]() ,同理
,同理![]() ,
,
所以![]() .
.
(2)由![]() 成等差数列,得
成等差数列,得![]()
所以弦长![]()
由(1)知显然斜率存在,由抛物线定义得![]()
故![]() ,解得
,解得![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
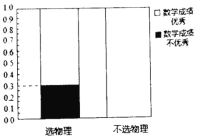
永乾教育寒假作业快乐假期延边人民出版社系列答案【题目】某省即将实行新高考,不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响,对该校2018级的1000名学生进行调查,收集到相关数据如下:
(1)根据以上提供的信息,完成![]() 列联表,并完善等高条形图;
列联表,并完善等高条形图;
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
(2)能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关?
附: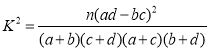
临界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【题目】在某外国语学校举行的![]() (高中生数学建模大赛)中,参与大赛的女生与男生人数之比为
(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖.按女生、男生用分层抽样的方法抽取
)的同学获奖.按女生、男生用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图如图所示.
人的成绩作为样本,得到成绩的频率分布直方图如图所示.
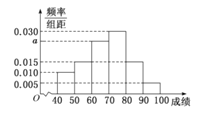
(Ⅰ)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)填写下面的![]() 列联表,并判断在犯错误的概率不超过
列联表,并判断在犯错误的概率不超过![]() 的前提下能否认为“获奖与女生、男生有关”.
的前提下能否认为“获奖与女生、男生有关”.
女生 | 男生 | 总计 | |
获奖 |
| ||
不获奖 | |||
总计 |
| ||
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中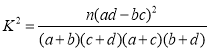 ,
,![]() .
.
【题目】“工资条里显红利,个税新政人民心”我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.2019年1月1日实施的个税新政主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)![]() 收人
收人![]() 个税起征点
个税起征点![]() 专项附加扣除;(3)专项附加扣除包括住房、子女教育和赡养老人等.新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如下:
专项附加扣除;(3)专项附加扣除包括住房、子女教育和赡养老人等.新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
缴税基数 | 每月应纳税所得额(含税) | 税率(%) | 每月应纳税所得额(含税) | 税率(%) |
1 | 不超过1500元的部分 | 3 | 不超过3000元的部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元的部分 | 30 | 超过35000元至55000元的部分 | 30 |
… | … | … | … | … |
随机抽取某市2020名同一收入层级的![]() 从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元,统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、既符合子女教育扣除又符合赡养老人扣除的人数之比是
从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元,统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、既符合子女教育扣除又符合赡养老人扣除的人数之比是![]() ;此外,他们均不符合其他专项附加扣除,新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.假设该市该收入层级的
;此外,他们均不符合其他专项附加扣除,新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.假设该市该收入层级的![]() 从业者都独自享受专项附加扣除,将预估的该市该收入层级的
从业者都独自享受专项附加扣除,将预估的该市该收入层级的![]() 从业者的人均月收入视为其个人月收入,根据样本估计总体的思想,解决如下问题:
从业者的人均月收入视为其个人月收入,根据样本估计总体的思想,解决如下问题:
(1)求在旧政策下该收入层级的![]() 从业者每月应纳的个税;
从业者每月应纳的个税;
(2)设该市该收入层级的![]() 从业者2019年月缴个税为X元,求X的分布列和期望;
从业者2019年月缴个税为X元,求X的分布列和期望;
(3)根据新旧个税方案,估计从2019年1月开始,经过多少个月,该市该收入层级的![]() 从业者各月少缴纳的个税之和就超过2019年的人均月收入?
从业者各月少缴纳的个税之和就超过2019年的人均月收入?