题目内容
在△ABC中,已知asinA+csinC-
asinC=bsinB.
(1)求B;
(2)若C=60°,b=2,求c与a.
| 2 |
(1)求B;
(2)若C=60°,b=2,求c与a.
(1)由已知 asinA+csinC-
asinC=bsinB,利用正弦定理得b2=a2+c2-
ac,…(3分)
再由余弦定理得b2=a2+c2-2ac•cosB,故cosB=
,∴B=45°.…(6分)
(2)由
=
,解得c=
.…(10分)
由余弦定理得:c2=a2+b2-2ab•cosC,
即a2-2a-2=0,∴a=
+1.…(14分)
| 2 |
| 2 |
再由余弦定理得b2=a2+c2-2ac•cosB,故cosB=
| ||
| 2 |
(2)由
| c |
| sinC |
| b |
| sinB |
| 6 |
由余弦定理得:c2=a2+b2-2ab•cosC,
即a2-2a-2=0,∴a=
| 3 |

练习册系列答案
相关题目
 .
. 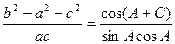
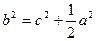 ,求
,求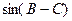 的值
的值 ABC中,
ABC中, ,
, ,面积为
,面积为 ,那么
,那么 的长度为( )
的长度为( )


