题目内容
在空间中,a,b是不重合的直线,α,β是不重合的平面,则下列条件中可推出a∥b的是:
A.a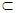 α,b α,b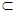 β α∥β β α∥β | B.a⊥α b⊥α |
C.a∥αb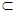 α α | D.a⊥α b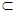 α α |
B
垂直于同一个平面的两条直线平行.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
题目内容
A.a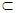 α,b α,b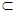 β α∥β β α∥β | B.a⊥α b⊥α |
C.a∥αb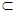 α α | D.a⊥α b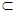 α α |

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案