题目内容
(本小题满分14分)
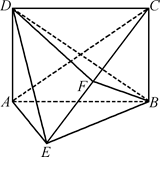
如图,在四棱锥E—ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,求证:
(1) AE∥平面BDF;
(2) 平面BDF⊥平面BCE.

如图,在四棱锥E—ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,求证:
(1) AE∥平面BDF;
(2) 平面BDF⊥平面BCE.
见解析。
本试题主要是考查了立体几何中线面的平行的判定和面面垂直的证明的运用。
(1)根据已知条件,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,设AC∩BD=G,连结FG,易知G是AC的中点,
因为 F是EC中点,所以在△ACE中,FG∥AE可知结论。
(2)因为 平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB,所以 BC⊥平面ABE,从而得到BC⊥AE,再利用线面垂直得到面面垂直的判定。
证明:(1) 设AC∩BD=G,连结FG,易知G是AC的中点,
因为 F是EC中点,所以 在△ACE中,FG∥AE.………2分
因为 AE?平面BDF,FG?平面BDF,
所以 AE∥平面BDF. ………………………………………6分
(2) 因为 平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB,所以 BC⊥平面ABE.………8分
因为 AE?平面ABE,所以 BC⊥AE.…………………………………………………………10分
又AE⊥BE,BC∩BE=B,所以 AE⊥平面BCE,又FG∥AE,
所以FG⊥平面BCE,……………………………………………………………………………12分
因为 FG?平面BDF,所以平面BDF⊥平面BCE.………………………………………………14分
(1)根据已知条件,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,设AC∩BD=G,连结FG,易知G是AC的中点,
因为 F是EC中点,所以在△ACE中,FG∥AE可知结论。
(2)因为 平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB,所以 BC⊥平面ABE,从而得到BC⊥AE,再利用线面垂直得到面面垂直的判定。
证明:(1) 设AC∩BD=G,连结FG,易知G是AC的中点,
因为 F是EC中点,所以 在△ACE中,FG∥AE.………2分
因为 AE?平面BDF,FG?平面BDF,
所以 AE∥平面BDF. ………………………………………6分
(2) 因为 平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB,所以 BC⊥平面ABE.………8分
因为 AE?平面ABE,所以 BC⊥AE.…………………………………………………………10分
又AE⊥BE,BC∩BE=B,所以 AE⊥平面BCE,又FG∥AE,
所以FG⊥平面BCE,……………………………………………………………………………12分
因为 FG?平面BDF,所以平面BDF⊥平面BCE.………………………………………………14分

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
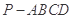 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.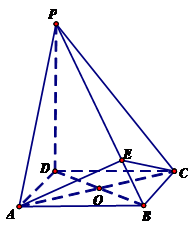
 ;
; 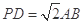 且
且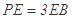 时,求AE与平面PDB所成的角的正切值.
时,求AE与平面PDB所成的角的正切值.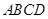 是矩形,
是矩形,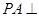 平面
平面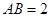 ,
,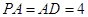 ,
,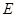 为
为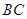 的中点.
的中点.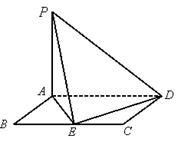
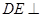 平面
平面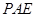 ;
;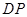 与平面
与平面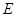 ,
,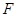 分别是正方形
分别是正方形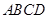 边
边 、
、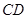 的中点,
的中点, 与
与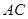 交于点
交于点 ,
,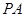 、
、 都垂直于平面
都垂直于平面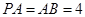 ,
,  ,
,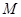 是线段
是线段
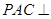 平面
平面 ;
; 平面
平面 ;
;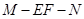 的余弦值.
的余弦值.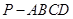 的底面为正方形,侧棱
的底面为正方形,侧棱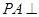 底面
底面 ,且
,且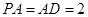 ,
,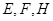 分别是线段
分别是线段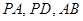 的中点.
的中点.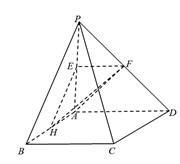
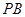 //平面
//平面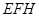 ;
;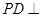 平面
平面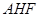 ;
;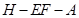 的大小.
的大小.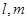 ,平面
,平面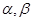 ,且
,且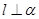 ,
,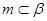 ,给出下列四个命题:
,给出下列四个命题: ∥
∥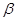 ,则
,则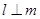 ;②若
;②若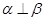 ,则
,则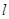 ∥
∥ ;④若
;④若 ,
,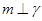 ,那么必有( )
,那么必有( )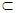 α,b
α,b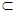 β α∥β
β α∥β