题目内容
(本题满分14分)如图,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且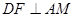 ,垂足为E,若将
,垂足为E,若将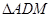 沿AM折起,使点D位于
沿AM折起,使点D位于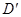 位置,连接
位置,连接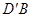 ,
,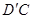 得四棱锥
得四棱锥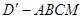 .
.
(1)求证: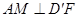 ;(2)若
;(2)若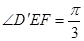 ,直线
,直线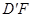 与平面ABCM所成角的大小为
与平面ABCM所成角的大小为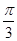 ,求直线
,求直线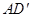 与平面ABCM所成角的正弦值.
与平面ABCM所成角的正弦值.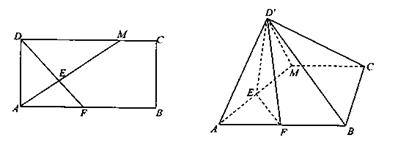
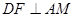 ,垂足为E,若将
,垂足为E,若将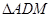 沿AM折起,使点D位于
沿AM折起,使点D位于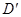 位置,连接
位置,连接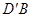 ,
,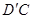 得四棱锥
得四棱锥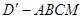 .
.(1)求证:
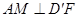 ;(2)若
;(2)若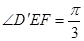 ,直线
,直线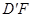 与平面ABCM所成角的大小为
与平面ABCM所成角的大小为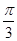 ,求直线
,求直线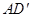 与平面ABCM所成角的正弦值.
与平面ABCM所成角的正弦值.
(1)证明:见解析;
(2)

(2)

(Ⅰ)根据图形折叠前后的关系,易证AM⊥面D′EF,得出AM⊥D′F.
(Ⅱ)由(Ⅰ)知,AM⊥面D′EF,所以平面ABCM⊥面D′EF,过D′作D′H⊥EF,则D′H⊥平面ABCM,,∠D′FH是直线D'F与平面ABCM所成角,∠D′AH是直线AD′与平面ABCM所成角在直角三角形D′AH求解即可.
(1)证明:∵AM⊥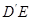 ,AM⊥EF,
,AM⊥EF,

(Ⅱ)由(Ⅰ)知,AM⊥面D′EF,所以平面ABCM⊥面D′EF,过D′作D′H⊥EF,则D′H⊥平面ABCM,,∠D′FH是直线D'F与平面ABCM所成角,∠D′AH是直线AD′与平面ABCM所成角在直角三角形D′AH求解即可.
(1)证明:∵AM⊥
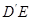 ,AM⊥EF,
,AM⊥EF,

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
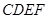 中,
中,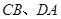 是梯形的高,
是梯形的高,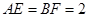 ,
,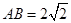 ,现将梯形沿
,现将梯形沿 ,且
,且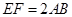 ,得一简单组合体
,得一简单组合体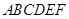 如图所示,已知
如图所示,已知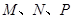 分别为
分别为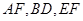 的中点.
的中点.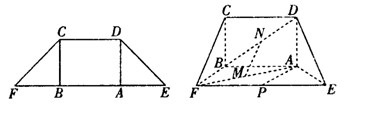
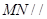 平面
平面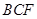 ;
; 平面
平面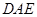 .
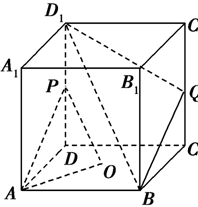
.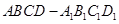 中,
中,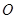 为底面
为底面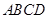 的中心,
的中心,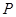 是
是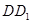 的中点,设
的中点,设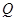 是
是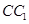 上的中点,求证:(1)
上的中点,求证:(1)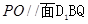 ;
;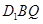 ∥平面
∥平面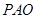 .
.
 中,
中,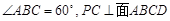 ,
,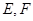 是
是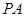 和
和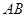 的中点.(Ⅰ)求证:
的中点.(Ⅰ)求证: 平面
平面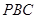 ;
;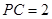 ,求
,求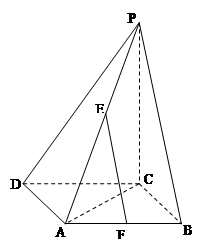
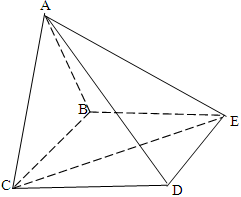
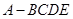 中,底面
中,底面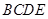 为矩形,侧面
为矩形,侧面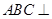 底面
底面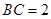 ,
,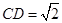 ,
,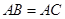 .
.
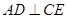 ;
; 与平面
与平面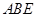 所成的角为
所成的角为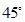 ,
, 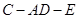 的余弦值.
的余弦值.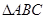 内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①
内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①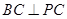 ;②
;②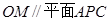 ;③点A到平面PBC距离就是△PAC的PC边上的高.④二面角P-BC-A大小不可能为450,其中真命题的个数为 ( )
;③点A到平面PBC距离就是△PAC的PC边上的高.④二面角P-BC-A大小不可能为450,其中真命题的个数为 ( )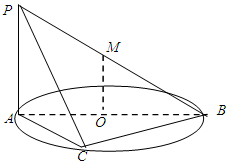
 ,
,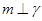 ,那么必有( )
,那么必有( )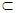 α,b
α,b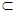 β α∥β
β α∥β