题目内容
【题目】某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,且将全班25人的成绩记为AI(I=1,2,…,25)由右边的程序运行后,输出n=10.据此解答如下问题: 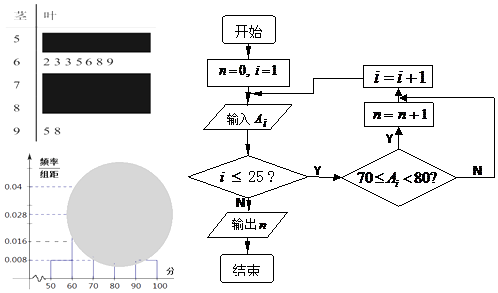
(Ⅰ)求茎叶图中破损处分数在[50,60),[70,80),[80,90)各区间段的频数;
(Ⅱ)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
【答案】解:(Ⅰ)由直方图知:在[50,60)之间的频率为0.008×10=0.08,
∴在[50,60)之间的频数为2;
由程序框图知:在[70,80)之间的频数为10
所以分数在[80,90)之间的频数为25﹣2﹣7﹣10﹣2=4;
(Ⅱ)分数在[50,60)之间的频率为2/25=0.08;
分数在[60,70)之间的频率为7/25=0.28;
分数在[70,80)之间的频率为10/25=0.40;
分数在[80,90)之间的频率为4/25=0.16;
分数在[90,100]之间的频率为2/25=0.08;
估计该班的测试成绩的众数75
设中位数为x,则0.08+0.28+0.04(x﹣70)=0.5,
解得x=73.5
【解析】(Ⅰ)由直方图先求出在[50,60)之间的频率及频数,由程序框图求出在[70,80)之间的频数,用样本容量相减,可得答案.(Ⅱ)计算各段的频率,进而得到频率最大的组中值即为众数,可估算平均数,求出频率的等分线,可得中位数.
【考点精析】本题主要考查了程序框图的相关知识点,需要掌握程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明才能正确解答此题.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案【题目】为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响,某农科所记录了5组昼夜温差与100颗种子发芽数,得到如表资料:
组号 | 1 | 2 | 3 | 4 | 5 |
温差x(°C) | 10 | 11 | 13 | 12 | 8 |
发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
该所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求出线性回归方程,再对被选取的2组数据进行检验.
(1)若选取的是第1组与第5组的两组数据,请根据第2组至第4组的数据,求出y关于x的线性回归方程 ![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(参考公式: ![]() =
= 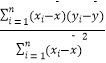 =
= 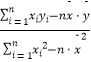 ,
, ![]() )
)