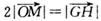题目内容
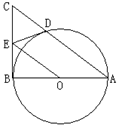
如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且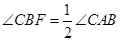 .
.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,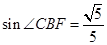 ,求BC和BF的长.
,求BC和BF的长.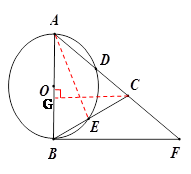
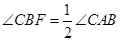 .
.(1)求证:直线BF是⊙O的切线;
(2)若AB=5,
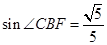 ,求BC和BF的长.
,求BC和BF的长.
(1)见解析;(2)BC=2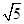 ,BF=
,BF=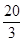
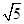 ,BF=
,BF=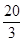
1)由已知条件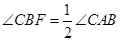 可判定直线BF与⊙O相切
可判定直线BF与⊙O相切
(2)在Rt△ANB中,利用边角关系求出BE的长,进而求出BC所以△AGC∽△FBA,利用对应边的比值相等求出PC,在利用勾股定理求出AE,则可求出.
证明:(1)证明:连结AE.
∵AB是⊙O的直径,
∴∠AEB=90°.
∴∠1=∠2=90°.
∵AB=AC
∴∠1=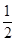 ∠CAB.
∠CAB.
∴∠CBF=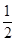 ∠CAB,
∠CAB,
∴∠1=∠CBF
∴∠CBF+∠2=90°.
即∠ABF=90°
∵AB是⊙O的直径,
∴直线BF是⊙O的切线.
(2)解:过点C作CG⊥AB于点G.
∵sin∠CBF=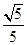 ,∠1=∠CBF,
,∠1=∠CBF,
∴sin∠1=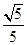
∵∠AEB=90°,AB=5,
∴BE=AB·sin∠1=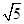
∵AB=AC,∠AEB=90°,
∴BC=2BE=2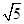
在Rt△ABE中,由勾股定理AE=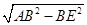 =2
=2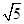
∴sin∠2=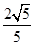 ,cos∠2=
,cos∠2=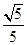 .
.
在Rt△CBG中,可求得GC=4,GB=2,
∴AG=3.
∵GC∥BF
∴△AGC∽△ABF.
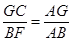
∴BF=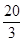
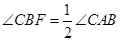 可判定直线BF与⊙O相切
可判定直线BF与⊙O相切(2)在Rt△ANB中,利用边角关系求出BE的长,进而求出BC所以△AGC∽△FBA,利用对应边的比值相等求出PC,在利用勾股定理求出AE,则可求出.
证明:(1)证明:连结AE.
∵AB是⊙O的直径,
∴∠AEB=90°.
∴∠1=∠2=90°.
∵AB=AC
∴∠1=
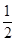 ∠CAB.
∠CAB.∴∠CBF=
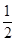 ∠CAB,
∠CAB,∴∠1=∠CBF
∴∠CBF+∠2=90°.
即∠ABF=90°
∵AB是⊙O的直径,
∴直线BF是⊙O的切线.
(2)解:过点C作CG⊥AB于点G.
∵sin∠CBF=
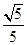 ,∠1=∠CBF,
,∠1=∠CBF,∴sin∠1=
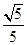
∵∠AEB=90°,AB=5,
∴BE=AB·sin∠1=
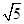
∵AB=AC,∠AEB=90°,
∴BC=2BE=2
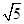
在Rt△ABE中,由勾股定理AE=
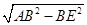 =2
=2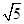
∴sin∠2=
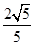 ,cos∠2=
,cos∠2=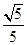 .
.在Rt△CBG中,可求得GC=4,GB=2,
∴AG=3.
∵GC∥BF
∴△AGC∽△ABF.
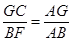
∴BF=

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
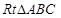 中,
中,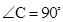 ,
,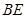 平分
平分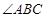 交
交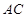 于点
于点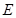 ,点
,点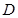 在
在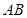 上,
上,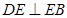 .
.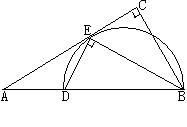
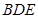 的外接圆的切线;
的外接圆的切线;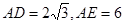 ,求
,求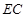 的长.
的长. 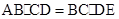
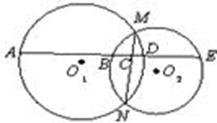
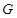 是△
是△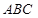 的外心,
的外心,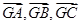 是三个单位向量,且2
是三个单位向量,且2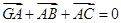 ,
,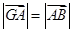 ,如图所示,△
,如图所示,△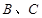 分别在
分别在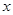 轴和
轴和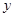 轴的非负半轴上移动,
轴的非负半轴上移动, 是坐标原点,则
是坐标原点,则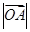 的最大值为 。
的最大值为 。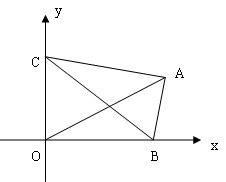
 和18
和18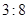 ,则另一弦的
,则另一弦的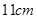
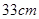
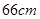
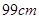
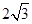 ,AB="BC=4," 则AC的长为
,AB="BC=4," 则AC的长为 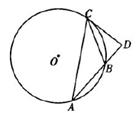
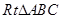 的直角边
的直角边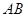 为直径作圆
为直径作圆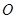 ,圆
,圆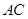 交于
交于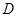 ,过
,过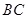 交于
交于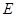 ,若
,若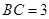 ,
,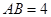 ,则
,则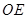 ="_________"
="_________" 
 外一点
外一点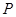 引圆的一条切线
引圆的一条切线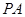 ,切点为
,切点为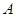 ,
,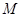 为
为 两点,且
两点,且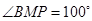 ,
, .
.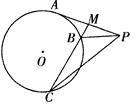
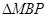 与
与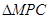 相似;
相似;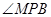 的大小.
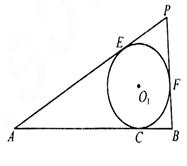
的大小.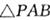 的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且
的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且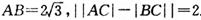 •
•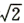 ,若l与曲线W相交于不同的两点G、H,点M满足
,若l与曲线W相交于不同的两点G、H,点M满足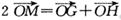 ,证明:
,证明: