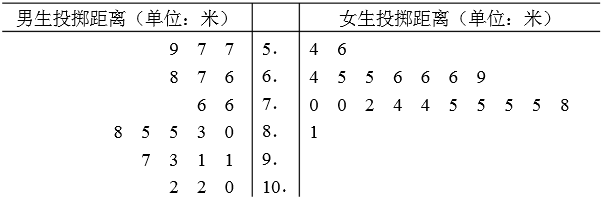
题目内容
3.某中学的一个研究性学习小组共有10名同学,其中男生x名(3≤x≤9),现从中选出3人参加一项调查活动,若至少有一名女生去参加的概率为f(x),则f(x)max=$\frac{119}{120}$.分析 列出关于f(x)的解析式,展开组合数整理成关于变量的一元三次函数形式,根据自变量的取值范围,对于一元三次函数求解,借助于导数求最值.
解答 解:由题意知本题是一个古典概型,
∵试验发生的所有事件是从10个人中选3人去参加某项调查活动共有C103种结果,
至少有一名女生去参加的对立事件是没有女生去参加,没有女生去参加共有C103-Cx3种结果,(3≤x≤9),
∴根据古典概型和对立事件的概率公式得到f(x)=1-$\frac{{C}_{x}^{3}}{{C}_{10}^{3}}$=1-$\frac{1}{720}$(x3-3x2+2x),(3≤x≤9),x∈N,
则f′(x)=-$\frac{1}{720}$(3x2-6x+2)=-$\frac{1}{720}$[3(x-1)2-1],
∵x∈[3,9],
3(x-1)2-1>0恒成立,
∴f′(x)在x∈[3,9]上恒小于0,
∴f(x)在[3,9]上为减函数.
∴f(3)最大,
∴f(x)max=f(3)=1-$\frac{{C}_{3}^{3}}{{C}_{10}^{3}}$=1-$\frac{1}{120}$=$\frac{119}{120}$,
故答案为:$\frac{119}{120}$.
点评 本题考查等可能事件的概率和导数,是一个综合题,可以作为高考题,对立事件包含于互斥事件,是对立事件一定是互斥事件,但是互斥事件不一定是对立事件,认识两个事件的关系,是解题的关键.

练习册系列答案
相关题目
13.某几何体的三视图如下图所示,则该几何体为( )
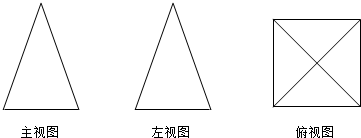

| A. | 三棱柱 | B. | 三棱锥 | C. | 圆锥 | D. | 四棱锥 |
1.已知方程ex-x+a=0(a为常数)有两个不等实根,则实数a的取值范围是( )
| A. | (0,1) | B. | (-1,0) | C. | (-∞,-1) | D. | (-∞,-1] |