题目内容
18.在△ABC内,a,b,c分别为角A,B,C所对的边,若a=$\sqrt{2}$,b=2,sinB+cosB=$\sqrt{2}$,则角A的大小为30°.分析 由条件由sinB+cosB=$\sqrt{2}$得1+2sinBcosB=2,即sin2B=1,根据三角形的内角和定理得到0<B<180°得到B的度数.利用正弦定理求出A即可.
解答 解:由sinB+cosB=$\sqrt{2}$得1+2sinBcosB=2,即sin2B=1,
因为0<B<180°,所以B=45°,b=2,所以在△ABC中,
由正弦定理得:$\frac{\sqrt{2}}{sinA}=\frac{2}{sin45°}$,
解得sinA=$\frac{1}{2}$,又a<b,所以A<B=45°,所以A=30°.
故答案为:30°.
点评 本题考查了三角恒等变换、已知三角函数值求解以及正弦定理,考查了同学们解决三角形问题的能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.过直线x+y=0上一点P作圆(x+1)2+(y-5)2=2的两条切线l1,l2,A,B为切点,当直线l1,l2关于直线y=-x对称时,∠APB=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
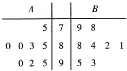 有A,B,C,D,E五位同学参加英语口语竞赛培训,现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据,这两组数据的样本茎叶图如图所示.
有A,B,C,D,E五位同学参加英语口语竞赛培训,现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据,这两组数据的样本茎叶图如图所示.