Question

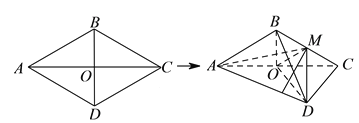
【题目】如图，菱形的边长为，，，将菱形沿对角线折起，得到三棱锥，点是棱的中点，．

（）求证：平面．

（）求证：平面平面．

（）求三棱锥的体积．

Answer 1

【答案】（）证明见解析;（）证明见解析;（）．

【解析】分析：（1）由题可知分别为中点，所以，得平面.

（2）由已知条件结合勾股定理得，又因为四边形为菱形得，所以平面，证得平面平面．

（3）由三棱锥的体积等于三棱锥的体积，从而得三棱锥的体积.

详解：（）证明：∵点是菱形的对角线交点，

∴是的中点，

又∵点是棱的中点，

∴是的中位线，，

∵平面，平面，

∴平面．

（）证明：由题意，

∵，

∴，，

又∵菱形中，，

，

∴平面，

∵平面，

∴平面平面．

（）∵三棱锥的体积等于三棱锥的体积由（）知平面，

∴是三棱锥的高，

，

∴．