题目内容
 某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185),得到的频率分布直方图如图所示.
某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185),得到的频率分布直方图如图所示.(1)分别求第3、4、5组的频率;
(2)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,问每一组分别抽几个人.
(3)在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.
考点:频率分布直方图,列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)直接根据频数、频率、样本容量三者之间的关系,得到第3组的频率为0.06×5=0.3,第4组的频率为0.04×5=0.2,第5组的频率为0.02×5=0.1;
(2)由分层抽样可以求得第3、4、5组分别抽取3人、2人、1人进入第二轮面试;
(3)从六位同学中抽两位同学有15种可能,抽取的是第4组的2位同学有9种可能,所以第4组的2位同学至少有一位同学入选的概率.
(2)由分层抽样可以求得第3、4、5组分别抽取3人、2人、1人进入第二轮面试;
(3)从六位同学中抽两位同学有15种可能,抽取的是第4组的2位同学有9种可能,所以第4组的2位同学至少有一位同学入选的概率.
解答:
解:(1)由题设可知,第3组的频率为0.06×5=0.3,
第4组的频率为0.04×5=0.2,
第5组的频率为0.02×5=0.1…(3分)
(2)第3组的人数为0.3×100=30,
第4组的人数为0.2×100=20,
第5组的人数为0.1×100=10
因为第3、4、5组共有60名学生,
所以利用分层抽样在60名学生中抽取6名学生,
每组抽取的人数分别为第3组:
×6=3,
第4组:
×6=2
第5组:
×6=1,
所以第3、4、5组分别抽取3人、2人、1人 …(7分)
(3)设第3组的3名学生分别为A1、A2、A3,
第4组的2名学生分别为B1、B2,
第5组的1名学生为C1,
则从6名学生中抽取两位学生有:
(A1,A2)、(A1,A3)、(A1,B1)、(A1,B2)、(A1,C1)、(A2,A3)、(A2,B1)、(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),共15种可能.
其中第4组的2位学生B1、B2至少有一位学生入选的有:
(A1,B1)、(A1,B2)、(A2,B1)、(A2,B2),(A3,B1),(A3,B2),(B1,B2),(B1,C1),(B2,C1),共9种可能,
所以第4组至少有一名学生被甲考官面试的概率为
=
…(12分)
第4组的频率为0.04×5=0.2,
第5组的频率为0.02×5=0.1…(3分)
(2)第3组的人数为0.3×100=30,
第4组的人数为0.2×100=20,
第5组的人数为0.1×100=10
因为第3、4、5组共有60名学生,
所以利用分层抽样在60名学生中抽取6名学生,
每组抽取的人数分别为第3组:
| 30 |
| 60 |
第4组:
| 20 |
| 60 |
第5组:
| 10 |
| 60 |
所以第3、4、5组分别抽取3人、2人、1人 …(7分)
(3)设第3组的3名学生分别为A1、A2、A3,
第4组的2名学生分别为B1、B2,
第5组的1名学生为C1,
则从6名学生中抽取两位学生有:
(A1,A2)、(A1,A3)、(A1,B1)、(A1,B2)、(A1,C1)、(A2,A3)、(A2,B1)、(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),共15种可能.
其中第4组的2位学生B1、B2至少有一位学生入选的有:
(A1,B1)、(A1,B2)、(A2,B1)、(A2,B2),(A3,B1),(A3,B2),(B1,B2),(B1,C1),(B2,C1),共9种可能,
所以第4组至少有一名学生被甲考官面试的概率为
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题重点考查频率分布直方图、概率求解方法、频率、频数、样本容量三者之间的关系等知识,属于中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
函数y=
sinx+cosx的一个单调递减区间是( )
| 3 |
A、[-
| ||||
| B、[-π,0] | ||||
C、[-
| ||||
D、[
|
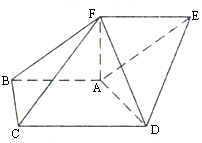 在五面体ABCDEF中,AB∥DC,∠BAD=
在五面体ABCDEF中,AB∥DC,∠BAD= 某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.