题目内容
已知数列{an}是首项为a1=
,公比q=
的等比数列.设bn+2=3log
an(n∈N*),数列{cn}满足cn=an•bn.(1)求证:数列{bn}成等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤
m2+m-1对一切正整数n恒成立,求实数m的取值范围.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
(2)求数列{cn}的前n项和Sn;
(3)若cn≤
| 1 |
| 4 |
考点:数列的求和,数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由等比数列的通项公式可得,an=
×(
)n-1=(
)n,bn+2=3log
(
)n=3n,即可得出bn,进而证明{bn}为等差数列.
(2)cn=an•bn=(3n-2)•(
)n,利用“错位相减法”即可得出;
(3)cn=an•bn=(3n-2)•(
)n,可得cn+1-cn=-9(
)n+1(n-1).即可得出(cn)max,由于cn≤
m2+m-1对一切正整数n恒成立,可得
m2+m-1≥(cn)max,解出即可.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
(2)cn=an•bn=(3n-2)•(
| 1 |
| 4 |
(3)cn=an•bn=(3n-2)•(
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
(1)证明:由已知可得,an=
×(
)n-1=(
)n,bn+2=3log
(
)n=3n,
∴bn=3n-2,bn+1-bn=3,
∴数列{bn}为等差数列,其中b1=1,d=3.
(2)解:cn=an•bn=(3n-2)•(
)n,
∴Sn=1×
+4×(
)2+…+(3n-2)•(
)n,
Sn=1×(
)2+4×(
)3+…+(3n-5)•(
)n+(3n-2)•(
)n+1,
两式相减可得:
Sn=
+3[(
)2+(
)3+…+(
)n]-(3n-2)•(
)n+1=
+3×
-(3n-2)×(
)n+1=
-(3n+2)•(
)n+1,
∴Sn=
-
×(
)n+1.
(3)解:cn=an•bn=(3n-2)•(
)n,
∴cn+1-cn=(3n+1)•(
)n+1-(3n-2)•(
)n=-9(
)n+1(n-1).
当n=1时,c2=c1;当n≥2时,cn+1<cn,
∴(cn)max=c1=c2=
.∵cn≤
m2+m-1对一切正整数n恒成立,∴
m2+m-1≥
,化为m2+4m-5≥0,
解得m≤-5或m≥1.
∴实数m的取值范围是m≤-5或m≥1.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∴bn=3n-2,bn+1-bn=3,
∴数列{bn}为等差数列,其中b1=1,d=3.
(2)解:cn=an•bn=(3n-2)•(
| 1 |
| 4 |
∴Sn=1×
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
两式相减可得:
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| ||||
|
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴Sn=
| 2 |
| 3 |
| 12n+8 |
| 3 |
| 1 |
| 4 |
(3)解:cn=an•bn=(3n-2)•(
| 1 |
| 4 |
∴cn+1-cn=(3n+1)•(
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
当n=1时,c2=c1;当n≥2时,cn+1<cn,
∴(cn)max=c1=c2=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解得m≤-5或m≥1.
∴实数m的取值范围是m≤-5或m≥1.
点评:本题考查了等比数列的通项公式及其前n项和公式、“错位相减法”,考查了恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
对两条不相交的空间直线a与b,必存在平面α,使得( )
| A、a?α,b?α |
| B、a?α,b∥α |
| C、a⊥α,b⊥α |
| D、a?α,b⊥α |
命题“若x2<1,则-1<x<1”的逆否命题是( )
| A、若x2≥1,则x≥1且x≤-1 |
| B、若-1<x<1,则x2<1 |
| C、若x>1或x<-1,则x2>1 |
| D、若x≥1或x≤-1,则x2≥1 |
有四个数a1,a2,a3,a4,前三个数成等比,积为64;后三个数成等差,和为6;则a1=( )
| A、9 | B、8 | C、16 | D、4 |
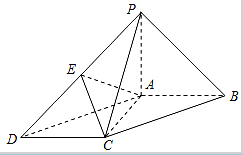 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点. 某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185),得到的频率分布直方图如图所示.
某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185),得到的频率分布直方图如图所示.