题目内容
【题目】在正四面体P﹣ABC体积为V,现内部取一点S,则 ![]() 的概率为( )
的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
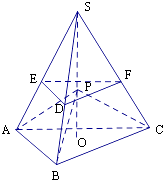
【解析】解:作出P在底面△ABC的射影为O,
若VS﹣ABC= ![]() VS﹣ABC,则高OS=
VS﹣ABC,则高OS= ![]() OP,
OP,
分别取PA、PB、PC上的点E、F、D,
并使SE=2EA,SF=2FC,SD=2DB,如图
并连结EF、FD、DE,则平面EFD∥平面ABC.
当点S在正四面体P﹣EFD内部运动时,
即此时S在三棱锥VP﹣ABC的中垂面DEF上,
满足VS﹣ABC< ![]() VP﹣ABC的点P位于在三棱锥VP﹣ABC的中垂面DEF以下的棱台内,
VP﹣ABC的点P位于在三棱锥VP﹣ABC的中垂面DEF以下的棱台内,
同理,VS﹣ABC> ![]() VP﹣ABC的S在距离ABC为
VP﹣ABC的S在距离ABC为 ![]() OS的平面以上的棱锥内,
OS的平面以上的棱锥内,
所以满足 ![]() 的棱台体积为(1
的棱台体积为(1 ![]() )﹣(1﹣
)﹣(1﹣ ![]() )=
)= ![]() ;
;
由几何概型,满足“ ![]() ”的概率为
”的概率为 ![]() ,
,
故选A.
【考点精析】本题主要考查了几何概型的相关知识点,需要掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等才能正确解答此题.

练习册系列答案
相关题目
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图像时,列表并填入了部分数据,如下表:
在某一个周期内的图像时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
|
|
|
|
| 0 | 5 | 0 | -5 | 0 |
(1)求出实数![]() ;
;
(2)求出函数![]() 的解析式;
的解析式;
(3)将![]() 图像上所有点向左平移
图像上所有点向左平移![]() 个单位长度,得到
个单位长度,得到![]() 图像,求
图像,求![]() 的图像离原点
的图像离原点![]() 最近的对称中心.
最近的对称中心.