题目内容
【题目】已知项数为![]() 的数列
的数列![]() 满足如下条件:①
满足如下条件:①![]() ;②
;②![]() .若数列
.若数列![]() 满足
满足![]() ,其中
,其中![]() ,则称
,则称![]() 为
为![]() 的“伴随数列”.
的“伴随数列”.
(1)数列1,3,5,7,9是否存在“伴随数列”,若存在,写出其“伴随数列”;若不存在,请说明理由;
(2)若![]() 为
为![]() 的“伴随数列”,证明:
的“伴随数列”,证明:![]() ;
;
(3)已知数列![]() 存在“伴随数列”
存在“伴随数列”![]() ,且
,且![]() ,
,![]() ,求m的最大值.
,求m的最大值.
【答案】(1) 不存在“伴随数列”,见解析 ;(2) 见解析;(3)33
【解析】
(1)根据“伴随数列”的定义检验即可判定;
(2)根据“伴随数列”的定义,结合数列的单调性讨论![]() 的符号即可得解;
的符号即可得解;
(3)根据数列![]() 和其“伴随数列”
和其“伴随数列”![]() 项的特征,结合单调性分析出
项的特征,结合单调性分析出![]() ,即可求解.
,即可求解.
(1)解:数列1,3,5,7,9不存在“伴随数列”
因为![]() ,
,
所以数列1,3,5,7,9不存在“伴随数列”.
(2)证明:因为![]() ,
,![]()
又因为![]() ,所以有
,所以有![]()
所以![]()
所以![]() 成立
成立
(3)![]() 1≤i
1≤i![]() j ≤m,都有
j ≤m,都有![]() ,
,
因为![]() ,
,![]() .
.
所以![]() ,
,
所以![]()
所以![]()
因为![]() ,
,
所以![]()
又![]()
![]() =
=![]()
所以![]() ,
,
所以![]()
又![]() ,
,
所以![]()
例如:![]() (
(![]() ),满足题意,
),满足题意,
所以m的最大值是33.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)求购买金额不少于45元的频率;
(2)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
女 | 18 | ||
合计 |
附:参考公式和数据: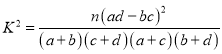 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
