题目内容
【题目】已知椭圆C:![]() (a>b>0)的顶点到直线l1:y=x的距离分别为
(a>b>0)的顶点到直线l1:y=x的距离分别为![]() 和
和![]() .
.
(1)求椭圆C的标准方程
(2)设平行于l1的直线l交C于A,B两点,且![]() ,求直线l的方程.
,求直线l的方程.
【答案】(1)![]() (2)直线
(2)直线![]() 的方程为
的方程为![]() 或
或![]()
【解析】
(1)根据直线l1的方程可知其与两坐标轴的夹角均为45°,进而得到![]() a
a![]() ,
,![]() b
b![]() ,即可求出C的方程;
,即可求出C的方程;
(2)设出直线l的方程,与椭圆方程联立,利用根与系数的关系结合|![]() |=|
|=|![]() |可得
|可得![]() 0,求出t即可.
0,求出t即可.
解:(1)由直线![]() 的方程知,直线
的方程知,直线![]() 与两坐标轴的夹角均为
与两坐标轴的夹角均为![]() ,
,
故长轴端点到直线![]() 的距离为
的距离为![]() ,短轴端点到直线
,短轴端点到直线![]() 的距离为
的距离为![]()
所以![]() a
a![]() ,
,![]() b
b![]() ,解得a=2,b=1,
,解得a=2,b=1,
所以椭圆![]() 的标准方程为
的标准方程为![]()
(2)依题设直线![]() 由
由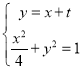 得:
得:![]()
判别式![]() 解得
解得![]()
设![]()
由韦达定理得:
由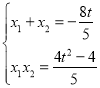 ,故
,故![]() ,
,
设原点为![]() ,
,![]() ,故
,故![]() ,
,
所以![]() ,即
,即![]()
解得:![]() ,满足
,满足![]() 且
且![]() ,
,
故所求直线![]() 的方程为
的方程为![]() 或
或![]()

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目