��Ŀ����
����Ŀ����ͼ,ij�������Ļ��ı߽���Բ��ΪO,ֱ��Ϊ1ǧ��Բ,��һ����һ��ֱ����·l,���м���һ����·AB(AB��ԲO��ֱ��),�滮�ڹ�·l��ѡ������P,Q,��������ֱ���͵�·PB,QA.�滮Ҫ��:��·PB,QA��������.��֪![]() ,
,![]() (CDΪ����),���OC=0.9,BD=1.2(��λ:ǧ��).��֪����·����ΪmԪ/ǧ��.�ڹ滮Ҫ����,����·�ܷ��õ���СֵΪ_____Ԫ.
(CDΪ����),���OC=0.9,BD=1.2(��λ:ǧ��).��֪����·����ΪmԪ/ǧ��.�ڹ滮Ҫ����,����·�ܷ��õ���СֵΪ_____Ԫ.

���𰸡�![]()
��������
���ݼ��ι�ϵ���ǵ�·���������������С���룬���ɵõ���С����.
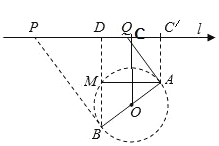
��ͼ������![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ��ȡ
��ȡ![]() ��Բ�Ľ���
��Բ�Ľ���![]() ��
��
����![]() ����
����![]() ��
��
����![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ��
��
����![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ��
��
����ͼ���ϵ�ɵã�ֱ���ϣ���![]() ���ĵ���
���ĵ���![]() �����߶β�����Բ�ڲ���
�����߶β�����Բ�ڲ���
��![]() �Ҳ�ĵ���
�Ҳ�ĵ���![]() ���ɵ��߶β�����Բ���ڲ���
���ɵ��߶β�����Բ���ڲ���
��̾���֮�ͼ�![]() ��
��
���ݼ��ι�ϵ��![]() ��
��![]() ��
��
����![]() ��
��
����![]() ��
��
![]() ������
������![]() ��
��
��С����Ϊ2.1ǧ��.
����·�ܷ��õ���СֵΪ![]() Ԫ.
Ԫ.
�ʴ�Ϊ��![]()

��ϰ��ϵ�д�
 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
�����Ŀ
