题目内容
已知函数 .
.
(1)若 ,求实数x的取值范围;
,求实数x的取值范围;
(2)求 的最大值.
的最大值.
(1) ;(2)
;(2) .
.
解析试题分析:(1)本题实质就是解不等式, ,当然这是含绝对值的不等式,因此我们应该根据绝对值的定义,按照绝对值符号里面的式子
,当然这是含绝对值的不等式,因此我们应该根据绝对值的定义,按照绝对值符号里面的式子 的正负性分类讨论,变为解两个二次不等式,最后还要把两个不等式的解集合并(即求并集),才能得到我们所要的结果;(2)本题实质就是求新函数
的正负性分类讨论,变为解两个二次不等式,最后还要把两个不等式的解集合并(即求并集),才能得到我们所要的结果;(2)本题实质就是求新函数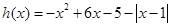 的最大值,同样由于式子中含有绝对值符号,因此我们按照绝对值符号里面的式子
的最大值,同样由于式子中含有绝对值符号,因此我们按照绝对值符号里面的式子 的正负性分类讨论去掉绝对值符号,变成求两个二次函数在相应区间上的最大值,最后在两个最大值中取最大的一个就是我们所要求的最大值;当然这题我们可以借助于(1)的结论,最大值一定在(1)中解集区间里取得,从而可以避免再去分类讨论,从而简化它的过程.
的正负性分类讨论去掉绝对值符号,变成求两个二次函数在相应区间上的最大值,最后在两个最大值中取最大的一个就是我们所要求的最大值;当然这题我们可以借助于(1)的结论,最大值一定在(1)中解集区间里取得,从而可以避免再去分类讨论,从而简化它的过程.
试题解析:(1)当 时,
时,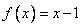 1分
1分
由 ,得
,得 ,
,
整理得 ,所以
,所以 ; 3分
; 3分
当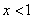 时,
时, , 4分
, 4分
由 ,得
,得 ,
,
整理得 ,由
,由 得
得 6分
6分
综上 的取值范围是
的取值范围是 ; 7分
; 7分
(2)由(1)知, 的最大值必在
的最大值必在 上取到, 9分
上取到, 9分
所以
所以当 时,
时, 取到最大值为
取到最大值为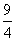 . 14分
. 14分
考点:(1)解不等式;(2)函数的最大值.

练习册系列答案
相关题目
 ,
, .
. ,判断函数
,判断函数 的奇偶性,并加以证明;
的奇偶性,并加以证明; 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围; 使得关于
使得关于 的方程
的方程 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数 的取值范围.
的取值范围.
 的定义域;
的定义域; 为何值时,函数值大于1.
为何值时,函数值大于1. (其中
(其中 是实数常数,
是实数常数, )
) ,函数
,函数 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求 的值;
的值; ,总有
,总有 ,求
,求 的取值范围;
的取值范围; ,
,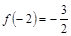 ,且对任意
,且对任意 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数 的取值范围.
的取值范围. ,函数
,函数 .
. 时,求
时,求 的最小值;
的最小值; 的范围,使得对于区间
的范围,使得对于区间 上的任意三个实数
上的任意三个实数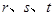 ,都存在以
,都存在以 为边长的三角形.
为边长的三角形. R).
R). )上是增函数,求实数a的取值范围;
)上是增函数,求实数a的取值范围; ,且f(x0)=3,求x0的值;
,且f(x0)=3,求x0的值; ,且在R上是减函数,求实数a的取值范围。
,且在R上是减函数,求实数a的取值范围。 的图象过点(2,0).
的图象过点(2,0).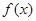 的奇偶性;
的奇偶性; 上的单调性,并给予证明;
上的单调性,并给予证明; 且
且 ,函数
,函数 ,
, ,记
,记 .
. 的定义域
的定义域 及其零点;
及其零点; 的方程
的方程 在区间
在区间 内仅有一解,求实数
内仅有一解,求实数 的取值范围.
的取值范围.