题目内容
已知函数f(x)=x3+ax-2,(a R).
R).
(l)若f(x)在区间(1,+ )上是增函数,求实数a的取值范围;
)上是增函数,求实数a的取值范围;
(2)若 ,且f(x0)=3,求x0的值;
,且f(x0)=3,求x0的值;
(3)若 ,且在R上是减函数,求实数a的取值范围。
,且在R上是减函数,求实数a的取值范围。
(1)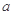 的取值范围是
的取值范围是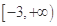 ;(2)
;(2)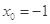 ,或
,或 ;(3)
;(3)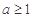 .
.
解析试题分析:(1)求导得: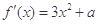 ,因为
,因为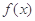 在区间
在区间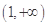 上是增函数,所以
上是增函数,所以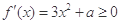 在
在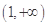 上恒成立,即
上恒成立,即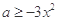 恒成立,只需
恒成立,只需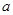 大于等于
大于等于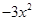 的最大值即可;
的最大值即可;
(2)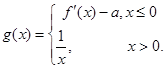 ,即
,即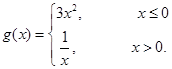 .分段函数求值就分情况分别求.
.分段函数求值就分情况分别求.
(3) 即
即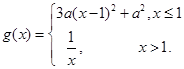 在
在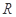 上是减函数,则两段都递减且
上是减函数,则两段都递减且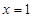 时两段的端点重合,由此即可求出
时两段的端点重合,由此即可求出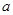 的取值范围.
的取值范围.
试题解析:(1)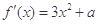 ,
,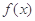 在区间
在区间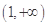 上是增函数,所以
上是增函数,所以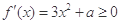 ,在
,在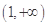 上恒成立,
上恒成立,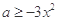 恒成立,所以
恒成立,所以 ,
,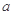 的取值范围是
的取值范围是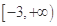 4分
4分
(2)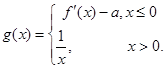 即
即 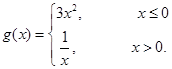
由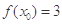 ,即
,即 或
或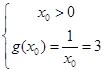
所以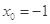 ,或
,或 . 9分
. 9分
(3) 即
即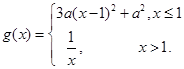 在
在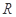 上是减函数,所以
上是减函数,所以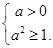
解之得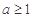 . 13分
. 13分
考点:1、函数的单调性及函数的值;2、分段函数.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 .
. 的定义域为集合B,若AÍB,求实数a的取值范围.
的定义域为集合B,若AÍB,求实数a的取值范围.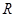 的函数
的函数
 的图象,并指出
的图象,并指出 有两个解,求出
有两个解,求出 的取值范围(只需简单说明,不需严格证明).
的取值范围(只需简单说明,不需严格证明). 为奇函数,且当
为奇函数,且当 时,
时, 求
求
 .
. ,求实数x的取值范围;
,求实数x的取值范围; 的最大值.
的最大值. (
( 为实常数).
为实常数). 图像上动点
图像上动点 到定点
到定点 的距离的最小值为
的距离的最小值为 ,求实数
,求实数 上是增函数,试用函数单调性的定义求实数
上是增函数,试用函数单调性的定义求实数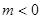 ,若不等式
,若不等式 在
在 有解,求
有解,求 的取值范围.
的取值范围.
 的定义域和值域;(2)若函数
的定义域和值域;(2)若函数 ,求
,求 的值。
的值。 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是 元.
元. .
.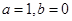 时,判断
时,判断 的奇偶性,并说明理由;
的奇偶性,并说明理由; 时,若
时,若 ,求
,求 的值;
的值; ,且对任何
,且对任何 不等式
不等式 恒成立,求实数
恒成立,求实数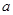 的取值范围.
的取值范围. ,其中
,其中 是实数,设
是实数,设 为该函数的图象上的两点,且
为该函数的图象上的两点,且 .
. 的单调区间;
的单调区间; 处的切线互相垂直,且
处的切线互相垂直,且 ,求
,求 的最小值;
的最小值;