Question

在四边形ABCD中，AB=2，BC=CD=4，AD=6，∠A+∠C=π．
（Ⅰ）求AC的长；
（Ⅱ）求四边形ABCD的面积．

Answer 1

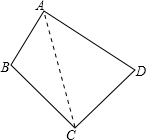解：（Ⅰ）如图，连接AC，
依题意可知：∠B+∠D=π，即∠D=π-∠B，
又AB=2，BC=CD=4，AD=6，
在△ABC中，由余弦定理得：AC²=AB²+BC²-2AB•BC•cosB=2²+4²-2×2×4cosB=20-16cosB，
在△ACD中，由余弦定理得：AC²=AD²+DC²-2AD•DC•cosD=6²+4²-2×6×4cosD=52-48cosD=52+48cosB，
由20-16cosB=52+48cosB，解得：cosB=-，
从而AC²=20-16cosB=28，即AC=2；…（6分）
（Ⅱ）由（Ⅰ）可知sinB=sinD=，
所以S_{四边形ABCD}=S_△ABC+S_△ACD=AB•BCsinB+AD•CDsinD=2+6=8．…（12分）
分析：（Ⅰ）根据题意画出图形，连接AC，由四边形的内角和为2π，根据∠A+∠C=π，得出∠B+∠D=π，用∠B表示出∠D，在三角形ABC中，利用余弦定理得到AC²=AB²+BC²-2AB•BC•cosB，将AB，BC的值代入表示出AC²，在三角形ADC中，由余弦定理得到AC²=AD²+DC²-2AD•DC•cosD，将AD，DC的值，以及表示出的∠D代入，利用诱导公式化简，根据AC相等，列出关系式，求出cosB的值，代入即可求出AC的值；
（Ⅱ）由∠D=π-∠B，得到sinB=sinD，利用三角形的面积公式求出三角形ABC的面积及三角形ADC的面积，根据四边形ABCD的面积=三角形ABC的面积+三角形ADC的面积，即可求出四边形ABCD的面积．
点评：此题考查了余弦定理，三角形的面积公式，诱导公式，以及四边形的内角和定理，熟练掌握定理及公式是解本题的关键．