题目内容
9.若锐角α、β满足cosα>sinβ则下列各式正确的是( )| A. | α+β<$\frac{π}{2}$ | B. | α+β=$\frac{π}{2}$ | C. | α+β>$\frac{π}{2}$ | D. | α>β |
分析 利用诱导公式以及正弦函数的单调性推出结果即可.
解答 解:锐角α、β满足cosα>sinβ,可得sin($\frac{π}{2}-α$)>sinβ.
可得$\frac{π}{2}-α>β$,∴α+β<$\frac{π}{2}$.
故选:A.
点评 本题考查三角函数的化简求值,正弦函数的单调性的应用,考查计算能力.

练习册系列答案
相关题目
19.如图三角形OAB为用斜二测画法所画的直观图,其原来平面图形的面积是( )
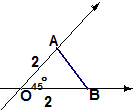

| A. | 4 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 8 |
14.已知m∈R,函数f(x)=$\left\{\begin{array}{l}{|3x+1|,x<0}\\{lo{g}_{3}x,x>0}\end{array}\right.$,g(x)=x2-2x+2m-1,若函数y=f(g(x))-m有6个零点,则实数m的取值范围是( )
| A. | (0,$\frac{5}{7}$) | B. | ($\frac{3}{7}$,$\frac{5}{7}$) | C. | (0,$\frac{3}{7}$) | D. | ($\frac{2}{7}$,1) |
1.椭圆的中心在原点,焦点在x轴上,焦距为4,离心率为$\frac{{\sqrt{2}}}{2}$,则该椭圆的方程为( )
| A. | $\frac{x^2}{32}$+$\frac{y^2}{16}$=1 | B. | $\frac{x^2}{12}$+$\frac{y^2}{8}$=1 | C. | $\frac{x^2}{8}$+$\frac{y^2}{4}$=1 | D. | $\frac{x^2}{12}$+$\frac{y^2}{4}$=1 |
18.已知sina+cosa=$\frac{\sqrt{3}}{2}$,且a∈(0,π),则sinacosa的值为( )
| A. | -$\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | ±$\frac{1}{8}$ | D. | -$\frac{1}{4}$ |