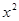题目内容
已知函数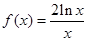
(1)求函数 在
在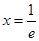 处的切线的斜率;
处的切线的斜率;
(2)求函数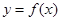 的最大值;
的最大值;
(3)设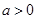 ,求函数
,求函数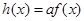 在
在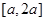 上的最大值.
上的最大值.
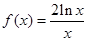
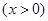
(1)求函数
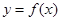 在
在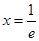 处的切线的斜率;
处的切线的斜率;(2)求函数
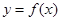 的最大值;
的最大值;(3)设
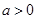 ,求函数
,求函数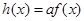 在
在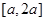 上的最大值.
上的最大值.(1)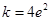 ,(2)
,(2)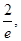 (3)
(3)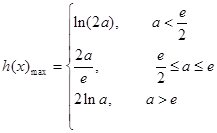
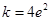 ,(2)
,(2)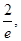 (3)
(3)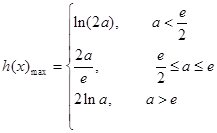
试题分析:(1)根据导数几何意义,函数在
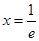 处的切线的斜率为函数在
处的切线的斜率为函数在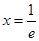 处的导数值,因此由
处的导数值,因此由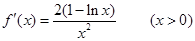 得
得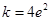 ,(2)利用导数求函数最值,需先分析函数单调性. 由
,(2)利用导数求函数最值,需先分析函数单调性. 由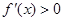 得
得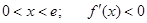 得
得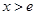 ,即
,即 在
在 上为增,在
上为增,在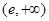 上为减∴
上为减∴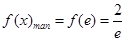 ,(3)同(2)一样,利用导数求函数最值,需先分析函数单调性. 由
,(3)同(2)一样,利用导数求函数最值,需先分析函数单调性. 由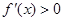 得
得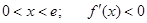 得
得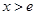 ,即
,即 在
在 上为增,在
上为增,在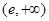 上为减.与(2)不同之处为,
上为减.与(2)不同之处为,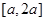 中是否包含e,需进行讨论. 当
中是否包含e,需进行讨论. 当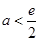 即
即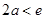 时,
时,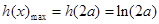 ,当
,当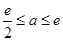 即
即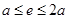 ,
,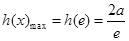 ,当
,当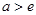 ,
,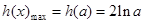 .
.解(1)
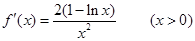 2分
2分当
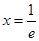 时,
时,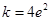 4分
4分(2)由
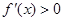 得
得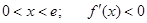 得
得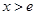 。
。即
 在
在 上为增,在
上为增,在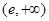 上为减 8分
上为减 8分∴
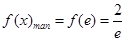 10分
10分(3)i)当
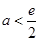 即
即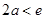 时,
时,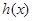 在
在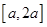 上为增,
上为增,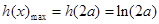 12分
12分ii)当
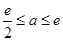 即
即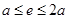 ,
,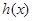 在
在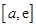 上为增,在
上为增,在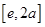 为减
为减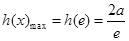 14分
14分iii)当
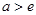 ,
, 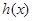 在
在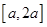 为减,
为减,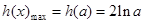
综上得,
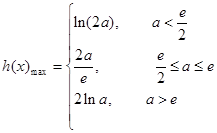 16分
16分
练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 .
. 时,求函数
时,求函数 的单调增区间;
的单调增区间;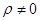 时,求函数
时,求函数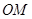 在区间
在区间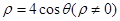 上的最小值;
上的最小值;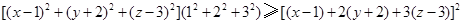 图象为曲线
图象为曲线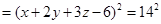 ,设点
,设点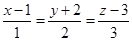 ,
,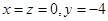 是曲线
是曲线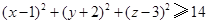 上不同的两点,点
上不同的两点,点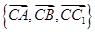 为线段
为线段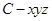 的中点,过点
的中点,过点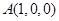 作
作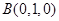 轴的垂线交曲线
轴的垂线交曲线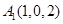 于点
于点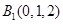 .试问:曲线
.试问:曲线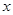 在点
在点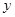 处的切线是否平行于直线
处的切线是否平行于直线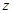 ?并说明理由.
?并说明理由.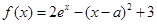 ,
,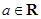 .
.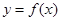 的图象在
的图象在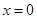 处的切线与
处的切线与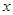 轴平行,求
轴平行,求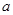 的值;
的值;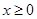 ,
,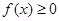 恒成立,求
恒成立,求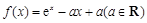 ,其图象与
,其图象与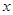 轴交于
轴交于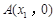 ,
,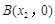 两点,且x1<x2.
两点,且x1<x2.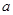 的取值范围;
的取值范围;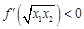 (
(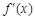 为函数
为函数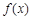 的导函数);
的导函数);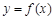 的图象上,且△ABC为等腰直角三角形,记
的图象上,且△ABC为等腰直角三角形,记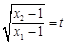 ,求
,求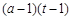 的值.
的值.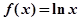 ,
,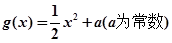 ,直线
,直线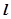 与 函数
与 函数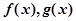 的图像都相切,且
的图像都相切,且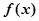 图像的切点的横坐标为1,则
图像的切点的横坐标为1,则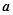 的值为 ( )
的值为 ( )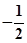
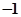
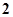
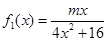 ,
,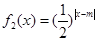 ,其中m∈R.
,其中m∈R.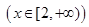 的单调性,并证明你的结论;
的单调性,并证明你的结论;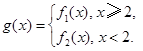 若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围.
若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围.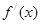 是函数
是函数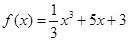 的导数,则
的导数,则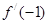 =
= 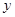 =
=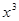
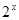 的导函数是( )
的导函数是( )