题目内容
若f(x)=2lnx﹣x2,则f′(x)>0的解集为( )
| A.(0,1) |
| B.(﹣∞,﹣1)∪(0,1) |
| C.(﹣1,0)∪(1,+∞) |
| D.(1,+∞) |
A
∵f(x)=2lnx﹣x2,
∴函数的定义域为(0,+∞),
则f'(x)=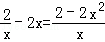 ,
,
由f'(x)=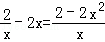 >0,
>0,
得x2﹣1<0,
即0<x<1,
即不等式的解集为(0,1),
故选:A.
∴函数的定义域为(0,+∞),
则f'(x)=
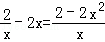 ,
,由f'(x)=
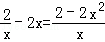 >0,
>0,得x2﹣1<0,
即0<x<1,
即不等式的解集为(0,1),
故选:A.

练习册系列答案
相关题目
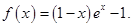
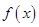 的最大值;
的最大值;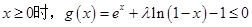 ,求
,求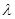 的取值范围.
的取值范围.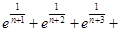 +
+
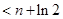 (n
(n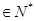 )
)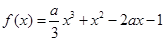 ,
,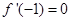 .
.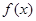 的单调区间;
的单调区间;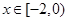 ,都有
,都有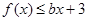 ,求
,求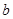 的取值范围.
的取值范围.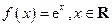 .
.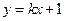 与
与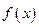 的反函数的图象相切,求实数k的值;
的反函数的图象相切,求实数k的值;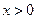 ,讨论曲线
,讨论曲线 与曲线
与曲线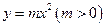 公共点的个数;
公共点的个数;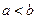 ,比较
,比较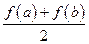 与
与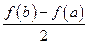 的大小,并说明理由.
的大小,并说明理由.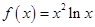 .
.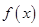 的单调区间;
的单调区间;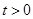 ,存在唯一的
,存在唯一的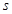 ,使
,使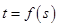 ;
;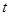 的函数为
的函数为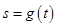 ,证明:当
,证明:当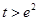 时,有
时,有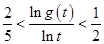 .
. 的大小关系 ( )
的大小关系 ( )
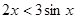

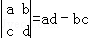 ,不等式
,不等式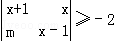 对一切x∈(0,1]恒成立,则实数m的最大值为( )
对一切x∈(0,1]恒成立,则实数m的最大值为( )
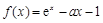 (
(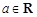 ).
).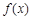 的单调区间;
的单调区间;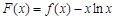 在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由;
在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由;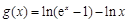 ,当
,当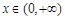 时,不等式
时,不等式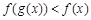 恒成立,求a的取值范围.
恒成立,求a的取值范围.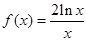
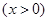
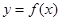 在
在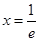 处的切线的斜率;
处的切线的斜率;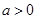 ,求函数
,求函数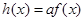 在
在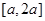 上的最大值.
上的最大值.