题目内容
【题目】出版商为了解某科普书一个季度的销售量![]() (单位:千本)和利润
(单位:千本)和利润![]() (单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
(单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2.4 | 3.1 | 4.6 | 5.3 | 6.4 | 7.1 | 7.8 | 8.8 | 9.5 | 10 |
| 18.1 | 14.1 | 9.1 | 7.1 | 4.8 | 3.8 | 3.2 | 2.3 | 2.1 | 1.4 |
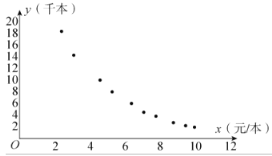
根据上述数据画出如图所示的散点图:
(1)根据图中所示的散点图判断![]() 和
和![]() 哪个更适宜作为销售量
哪个更适宜作为销售量![]() 关于利润
关于利润![]() 的回归方程类型?(给出判断即可,不需要说明理由)
的回归方程类型?(给出判断即可,不需要说明理由)
(2)根据(1)中的判断结果及参考数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)根据回归方程设该科普书一个季度的利润总额为![]() (单位:千元),当季销售量
(单位:千元),当季销售量![]() 为何值时,该书一个季度的利润总额预报值最大?(季利润总额=季销售量×每本书的利润)
为何值时,该书一个季度的利润总额预报值最大?(季利润总额=季销售量×每本书的利润)
参考公式及参考数据:
①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的公式分别为
的斜率和截距的公式分别为 .
.
②参考数据:
|
|
|
|
|
|
|
6.50 | 6.60 | 1.75 | 82.50 | 2.70 |
|
|
表中![]() .另:
.另:![]() .计算时,所有的小数都精确到0.01.
.计算时,所有的小数都精确到0.01.
【答案】(1))![]() 更适宜(2)
更适宜(2)![]() (3)季销量
(3)季销量![]() 千本时,季利润总额预报值最大
千本时,季利润总额预报值最大
【解析】
(1)根据散点图对应的图象特征判断.
(2)采用换元法令![]() ,先建立
,先建立![]() 关于
关于![]() 的线性回归方程,再将
的线性回归方程,再将![]() 代入求解.
代入求解.
(3)根据题意建立函数模型![]() ,再利用导数法求解.
,再利用导数法求解.
(1)![]() 更适宜作为销售量
更适宜作为销售量![]() 关于利润
关于利润![]() 的回归方程类型;
的回归方程类型;
(2)令![]() ,先建立
,先建立![]() 关于
关于![]() 的线性回归方程,
的线性回归方程,
由于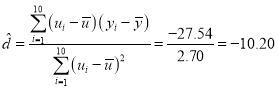 ,
,
![]() ,
,
所以![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,
,
即![]() 关于
关于![]() 的回归方程为
的回归方程为![]() .
.
(3)由题意得![]() ,
,![]() ,
,
令![]() 即
即![]() ,解得
,解得![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
所以当![]() 时,即季销量
时,即季销量![]() 千本时,季利润总额预报值最大.
千本时,季利润总额预报值最大.

 名校课堂系列答案
名校课堂系列答案【题目】随着我国经济的发展,居民收入逐年增长.某地区2014年至2018年农村居民家庭人均纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
人均纯收入 | 5 | 6 | 7 | 8 | 10 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2014年至2018年该地区农村居民家庭人均纯收入的变化情况,并预测2019年该地区农村居民家庭人均纯收入为多少?
附:回归直线的斜率和截距的最小二乘估计公式分别为 .
.