题目内容
【题目】在平面立角坐标系
中，过点
的圆的圆心
在
轴上，且与过原点倾斜角为
的直线
相切.
(1)求圆的标准方程；
(2)点
在直线
上，过点作圆的切线
、
，切点分别为
、
，求经过、、、四点的圆所过的定点的坐标.
【答案】（1）
（2）经过
、
、
、
四点的圆所过定点的坐标为
、
【解析】
(1)先算出直线方程，根据相切和过点
，圆心在
轴上联立方程解得答案.
(2) 取线段
的中点
，经过、、、四点的圆是以线段为直径的圆，设点的坐标为
，则点的坐标为
，将圆方程表示出来，联立方程组解得答案.
(1)由题意知，直线
的方程为
，整理为一般方程可得
由圆的圆心在轴上，可设圆的方程为
，
由题意有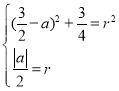
，解得：
，
，
故圆的标准方程为.
(2)由圆的几何性质知，
，
，取线段的中点，由直角三角形的性质可知
，故经过、、、四点的圆是以线段为直径的圆，
设点的坐标为，则点的坐标为
有
则以为直径的圆的方程为：
，整理为
可得
.
令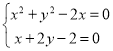
，解得
或
，
故经过、、、四点的圆所过定点的坐标为、.
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
