题目内容
已知M是满足下列条件的集合:①0∈M,1∈M;②若x,y∈M,则x-y∈M;③若x∈M且x≠0,则
∈M;
(1)判断
∈M是否正确,说明理由;
(2)证明:“x∈Z”是“x∈M”的充分条件,其中Z是正整数数集;
(3)证明:若x,y∈M,则xy∈M.
| 1 |
| x |
(1)判断
| 1 |
| 3 |
(2)证明:“x∈Z”是“x∈M”的充分条件,其中Z是正整数数集;
(3)证明:若x,y∈M,则xy∈M.
考点:必要条件、充分条件与充要条件的判断,元素与集合关系的判断
专题:集合,简易逻辑
分析:(1)由①②容易得到3∈M,所以由③得到
∈M;
(2)x∈M,能得到-x∈M,由已知条件知0∈M,所以只要证明任意的正整数x∈M即可得到任意的整数x∈M,可考虑用数学归纳法来证:1,2∈M,假设k∈M,则k-(-1)=k+1∈M,所以根据数学归纳法对任意正整数x∈M,所以便得到x∈Z是x∈M的充分条件;
(3)先构造出xy=
-
,所以可证明:若x,y∈M,则x2∈M,x+y∈M.先证明x2∈M,设x∈M,x≠0,则得到
∈M,1x-1∈M,
∈M,所以
-
=
∈M,所以x-x2∈M,所以得到x-(x-x2)=x2∈M,由前面知,x+y∈M,
+
=
∈M,所以
∈M,所以便可得到
,
∈M,所以得到
-
=xy∈M.
| 1 |
| 3 |
(2)x∈M,能得到-x∈M,由已知条件知0∈M,所以只要证明任意的正整数x∈M即可得到任意的整数x∈M,可考虑用数学归纳法来证:1,2∈M,假设k∈M,则k-(-1)=k+1∈M,所以根据数学归纳法对任意正整数x∈M,所以便得到x∈Z是x∈M的充分条件;
(3)先构造出xy=
| (x+y)2 |
| 2 |
| x2+y2 |
| 2 |
| 1 |
| x |
| 1 |
| x-1 |
| 1 |
| x |
| 1 |
| x-1 |
| 1 |
| x(1-x) |
| 1 |
| x |
| 1 |
| x |
| 2 |
| x |
| x |
| 2 |
| (x+y)2 |
| 2 |
| x2+y2 |
| 2 |
| (x+y)2 |
| 2 |
| x2+y2 |
| 2 |
解答:
解:(1)
∈M正确,证明如下:
由①0∈M,1∈M,由②知0-1=-1∈M;
∴1-(-1)=2∈M,2-(-1)=3∈M;
由③知
∈M;
(2)证明:由②知,若x∈M,则0-x=-x∈M,故只需证明任意正整数x∈M即可;
由(1)知,2∈M,假设正整数k∈M,则k-(-1)=k+1∈M;
∴由数学归纳法知:任意正整数x∈M;
即x∈Z,是x∈M的充分条件;
(3)证明:先证:若x∈M,则x2∈M:
由②知,若x∈M,且x≠0,∵1∈M,则x-1∈M;
由③知,
∈M,
∈M;
∴
-
=
∈M,∴x-x2∈M;
由②知,x-(x-x2)=x2∈M;
再证:若x,y∈M,则x+y∈M:
0-y=-y∈M,∴x-(-y)=x+y∈M;
∴
+
=
∈M;
∴
∈M;
∴由前面知:(x+y)2,x2,y2,
,
∈M;
∴
-
=xy∈M.
| 1 |
| 3 |
由①0∈M,1∈M,由②知0-1=-1∈M;
∴1-(-1)=2∈M,2-(-1)=3∈M;
由③知
| 1 |
| 3 |
(2)证明:由②知,若x∈M,则0-x=-x∈M,故只需证明任意正整数x∈M即可;
由(1)知,2∈M,假设正整数k∈M,则k-(-1)=k+1∈M;
∴由数学归纳法知:任意正整数x∈M;
即x∈Z,是x∈M的充分条件;
(3)证明:先证:若x∈M,则x2∈M:
由②知,若x∈M,且x≠0,∵1∈M,则x-1∈M;
由③知,
| 1 |
| x |
| 1 |
| x-1 |
∴
| 1 |
| x |
| 1 |
| x-1 |
| 1 |
| x(1-x) |
由②知,x-(x-x2)=x2∈M;
再证:若x,y∈M,则x+y∈M:
0-y=-y∈M,∴x-(-y)=x+y∈M;
∴
| 1 |
| x |
| 1 |
| x |
| 2 |
| x |
∴
| x |
| 2 |
∴由前面知:(x+y)2,x2,y2,
| (x+y)2 |
| 2 |
| x2+y2 |
| 2 |
∴
| (x+y)2 |
| 2 |
| x2+y2 |
| 2 |
点评:考查对给出的新信息的运用,以及数学归纳法在证明正整数问题的运用,而想到xy=
-
是求解本题的关键.
| (x+y)2 |
| 2 |
| x2+y2 |
| 2 |

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
若定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,则有( )
| A、f(-25)<f(80)<f(11) |
| B、f(11)<f(80)<f(-25) |
| C、f(-25)<f(11)<f(80) |
| D、f(80)<f(11)<f(-25) |
函数y=
的定义域是( )
| 1 |
| x-1 |
| A、(1,+∞) |
| B、R |
| C、(-∞,1)∪(1,+∞) |
| D、(-∞,1) |
在△ABC中,D是BC边上的一点,
=λ(
+
).|
|=2,|
=4,若记
=
,
=
,则用
,
表示
所得的结果为( )
| AD |
| ||
|
|
| ||
|
|
| AB |
| AC| |
| AB |
| a |
| AC |
| b |
| a |
| b |
| BD |
A、
| ||||||||
B、
| ||||||||
C、-
| ||||||||
D、
|
已知直线l1:3ax+(a2-1)y+6=0与l2:x+(a-1)y=0平行,则实数a的取值为( )
A、.1或-
| ||
B、
| ||
| C、1 | ||
D、
|
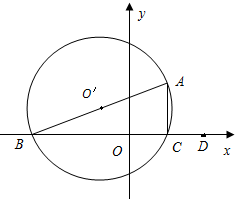 如图,在平面直角坐标系中,△ABC内接于⊙O,其中AB为⊙O直径,A(1,3),B(-3,0),C(1,0).
如图,在平面直角坐标系中,△ABC内接于⊙O,其中AB为⊙O直径,A(1,3),B(-3,0),C(1,0).