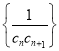题目内容
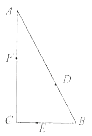
【题目】已知四边形ABCD内接于圆O
(1)若AB=2,BC=6,CD=4,AC=8,求BD
(2)若AC=![]() ,BC=
,BC=![]() +1,∠ADB=
+1,∠ADB=![]() ,求AD2+DC2的取值范围
,求AD2+DC2的取值范围
【答案】(1)BD=![]() .(2)[
.(2)[ ![]() ].
].
【解析】试题分析:(1)由![]() 四点共圆,所以
四点共圆,所以![]() ,则在
,则在![]() 和
和![]() 中,由余弦定理得
中,由余弦定理得
![]() =
= ![]() ,可求
,可求![]() ,同理可求
,同理可求![]() ;
;
(2)由题∠ADB=![]() ,可得∠ACB=
,可得∠ACB=![]()
![]() 中由余弦定理得
中由余弦定理得![]() 。由余弦定理可得cos∠ABC==
。由余弦定理可得cos∠ABC==![]()
所以∠ABC=![]() ,∠ADC=
,∠ADC=![]()
在![]() C中,由正弦定理得
C中,由正弦定理得![]() =
=![]() =
=![]() =2
=2![]()
所以![]() 令
令![]() ,则
,则![]()
![]() 整理化简,由辅助角公式可求
整理化简,由辅助角公式可求![]() 的取值范围
的取值范围
试题解析:(1)ABCD四点共圆,所以∠ABC+∠ADC=π,∠BAD+∠BCD=π
在△ABC和△ADC中,由余弦定理得
cos∠ABC=![]() =
=![]() =-cos∠ADC
=-cos∠ADC
可求得=4
同理,在△ABC和△ADC中有
cos∠BAD=![]() =
=![]() =-cos∠BCD
=-cos∠BCD
可求得BD=![]() .
.
(2)∠ADB=![]() ,∴∠ACB=
,∴∠ACB=![]()
△ABC中由余弦定理得,AB2=AC2+BC2-2AC·BCcos![]()
所以AB=2
cos∠ABC=![]() =
=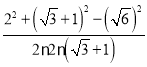 ==
==![]()
所以∠ABC=![]() ,∠ADC=
,∠ADC=![]()
在△ADC中,由正弦定理得![]() =
=![]() =
=![]() =2
=2![]()
所以AD=2![]() sin∠ACD,CD=2
sin∠ACD,CD=2![]() sin∠CAD
sin∠CAD
令∠ACD=θ,则∠CAD=![]() -θ
-θ
AD2+DC2=(2![]() sinθ)2+[2
sinθ)2+[2![]() sin(
sin(![]() -θ)]2
-θ)]2
=8(![]() sin2θ+
sin2θ+![]() cos2θ-
cos2θ-![]() sinθcosθ)
sinθcosθ)
=8(![]() -
-![]() +
+![]() )
)
=8-(2cos2θ+2![]() sin2θ)
sin2θ)
=8-![]() sin(2θ+
sin(2θ+![]() )
)
θ∈(0![]() ),2θ+
),2θ+![]() ∈(
∈(![]() ,
,![]() )
)
所以AD2+DC2∈[![]() ].
].

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目