题目内容
如图, 在三棱锥 中,
中,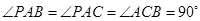 .
.
(1)求证:平面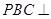 平面
平面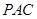 ;
;
(2)若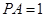 ,
,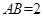 ,当三棱锥
,当三棱锥 的体积最大时,求
的体积最大时,求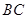 的长.
的长.
(1)详见解析;(2)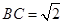 .
.
解析试题分析:(1)利用已知条件先证明 平面
平面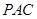 ,然后再利用平面与平面垂直的判定定理证明平面
,然后再利用平面与平面垂直的判定定理证明平面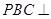 平面
平面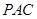 ;(2)方法1:利用(1)中的提示信息说明
;(2)方法1:利用(1)中的提示信息说明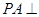 平面
平面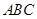 ,将
,将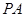 视为三棱锥
视为三棱锥 的高,设
的高,设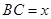 ,将底面积用
,将底面积用 表示出来,最后将三棱锥
表示出来,最后将三棱锥 用以
用以 的代数式进行表示,并结合基本不等式求最大值;方法2:由于
的代数式进行表示,并结合基本不等式求最大值;方法2:由于 为直角三角形,将
为直角三角形,将 的面积用以
的面积用以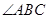 为自变量的三角函数表示,最终将三棱锥
为自变量的三角函数表示,最终将三棱锥 的体积用三角函数进行表示,最后利用三角函数的相关方法求体积的最大值.
的体积用三角函数进行表示,最后利用三角函数的相关方法求体积的最大值.
试题解析:(1)证明:因为 ,所以
,所以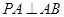 ,
,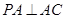 . 1分
. 1分
因为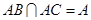 ,所以
,所以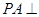 平面
平面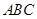 . 2分
. 2分
因为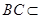 平面
平面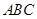 ,所以
,所以 . 3分
. 3分
因为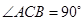 ,所以
,所以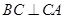 . 4分
. 4分
因为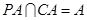 ,所以
,所以 平面
平面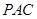 . 5分
. 5分
因为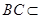 平面
平面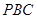 ,所以平面
,所以平面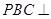 平面
平面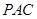 . 6分
. 6分
(2)方法1:由已知及(1)所证可知,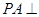 平面
平面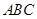 ,
,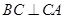 ,
,
所以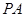 是三棱锥
是三棱锥 的高. 7分
的高. 7分
因为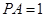 ,
,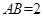 ,设
,设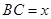
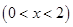 , 8分
, 8分
所以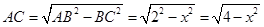 . 9分
. 9分
因为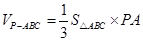
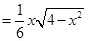 10分
10分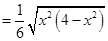
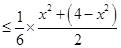 11分
11分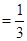 . 12分
. 12分
当且仅当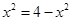 ,即
,即 时等号成立. 13分
时等号成立. 13分
所以当三棱锥 的体积最大时,
的体积最大时,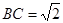 . 14分
. 14分
方法2:由已知及(1)所证可知,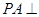 平面
平面
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的底面
的底面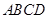 是正方形,棱
是正方形,棱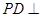 底面
底面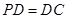 =1,
=1, 是
是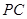 的中点.
的中点.
 平面
平面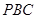 ;
; 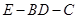 的余弦值.
的余弦值. 、
、 为圆柱
为圆柱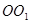 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, 、
、 分别是
分别是 的中点,
的中点,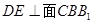 .
.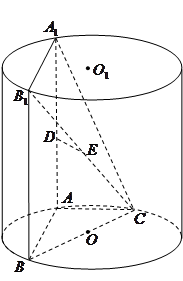
 ;
; ;
;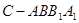 与圆柱
与圆柱 中,
中, 平面
平面 .
.
 的充分条件,并给予证明;
的充分条件,并给予证明; ,②
,② ;③
;③ 为锐角,求平面
为锐角,求平面 与平面
与平面 所成锐二面角
所成锐二面角 的取值范围.
的取值范围. 中,
中, 平面
平面 ,
, 平面
平面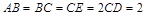 ,
, .
.
 平面
平面 ;
; 的大小.
的大小. ,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点
,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点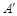 ,连结A¢B.
,连结A¢B.
 中,
中,
 底面
底面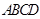 ,
, ,
, ,
, .
. 平面
平面 ;
;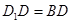 ,求四棱锥
,求四棱锥 的体积.
的体积.
 的4个顶点都在球
的4个顶点都在球 的表面上,
的表面上, 为球
为球 为球面上一点,且
为球面上一点,且 平面
平面  ,点
,点 为
为 的中点.
的中点.  平面
平面 ;
; 到平面
到平面 的距离.
的距离.
 中,
中, ,
, ,
, 分别是
分别是 上的点,
上的点, ,
, 为
为 的中点.将
的中点.将 沿
沿 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥 ,其中
,其中 .
.
 平面
平面 ;
; 的平面角的余弦值.
的平面角的余弦值.