题目内容
如图,边长为a的正方形ABCD中,点E、F分别在AB、BC上,且 ,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点
,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点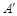 ,连结A¢B.
,连结A¢B.
(Ⅰ)判断直线EF与A¢D的位置关系,并说明理由;
(Ⅱ)求二面角F-A¢B-D的大小.
(Ⅰ)异面垂直;(Ⅱ)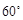 .
.
解析试题分析:(Ⅰ)先证明A¢D⊥面A¢EF即可得EF与A¢D的位置关系是异面垂直;
(Ⅱ)先作出并证明ÐOHF是二面角F-A¢B-D的平面角,再利用解三角形的方法求出ÐOHF的大小.
试题解析:(Ⅰ)A¢D⊥EF. 1分
证明如下:因为A¢D⊥A¢E,A¢D⊥A¢F,
所以A¢D⊥面A¢EF,又EFÌ面A¢EF,
所以A¢D⊥EF. 直线EF与A¢D的位置关系是异面垂直 4分
直线EF与A¢D的位置关系是异面垂直 4分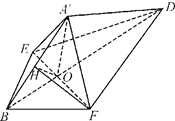
(Ⅱ)方法一、设EF、BD相交于O,连结A¢O,作FH⊥A¢B于H,
连结OH, 因为EF⊥BD, EF⊥A¢D.
所以EF⊥面A¢BD,A¢BÌ面A¢BD, 所以A¢B⊥EF,又A¢B⊥FH,
故A¢B⊥面OFH,OHÌ面OFH, 所以A¢B⊥OH,
故ÐOHF是二面角F-A¢B-D的平面角.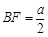 ,A¢E=A¢F=
,A¢E=A¢F=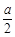 ,EF=
,EF=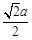 ,则
,则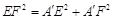 ,
,
所以,△A¢EF是直角三角形,则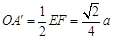 ,
,
则 ,
,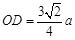 ,∴
,∴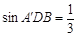 ,
,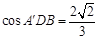 ,
,
则A¢B=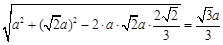 ,所以
,所以 ,
,
所以, tanÐOHF=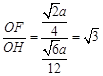 ,故ÐOHF=
,故ÐOHF=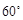 .
.
所以二面角F-A¢B-D的大小为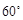 . 12分
. 12分
方法二、设EF、BD相交于O,连结A¢O,作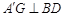 于G,可得A¢G⊥面BEDF,
于G,可得A¢G⊥面BEDF,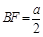 ,A¢E=A¢F=
,A¢E=A¢F=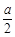 ,EF=
,EF=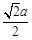 ,则
,则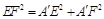 ,
,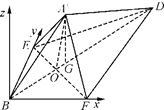
所以,△A¢EF是直角三角形,则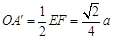 ,
,
则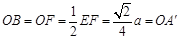 ,则
,则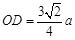 ,
,
∴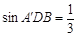 ,
,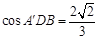 ,
,
所以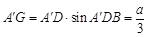 ,
,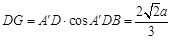 ,则
,则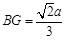 ,
,
分别以BF、BE为空间直角坐标系的x、y轴,建立如图坐标系,则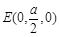 ,
,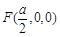 ,
, 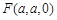 ,
,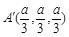 ,故
,故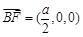 ,
,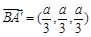 ,
, ,
,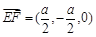 ,
,
因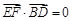 ,
,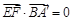 ,故面A¢BD的一个法向量
,故面A¢BD的一个法向量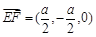 ,
,
设面A¢BF的一法向量为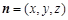 ,则
,则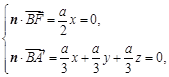 取
取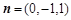 ,
,
设二面角F-A¢B-D的平面角为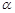 ,则
,则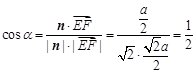 ,∴
,∴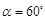 ,
,
故二面角F-A¢B-D的大小为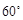 . 12分
. 12分
考点:1.直线与平面的位置关系; 2.二面角.

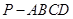 中,
中,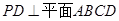 ,
,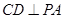 ,
, 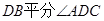 ,
,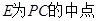 ,
,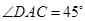 ,
,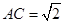 .
.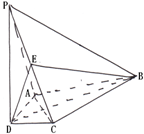
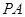 ∥
∥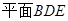 ;
;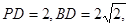 求四棱锥
求四棱锥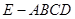 的体积
的体积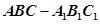 中,
中,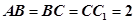 ,
,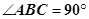 ,D是AC的中点.
,D是AC的中点.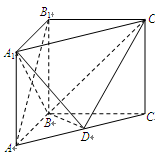
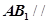 平面
平面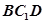 ;
;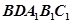 的体积.
的体积.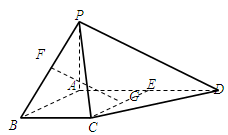
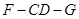 的正切值.
的正切值. 中,
中,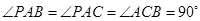 .
.
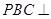 平面
平面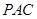 ;
;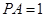 ,
,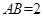 ,当三棱锥
,当三棱锥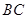 的长.
的长.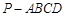 中,底面
中,底面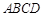 是矩形,四条侧棱长均相等.
是矩形,四条侧棱长均相等.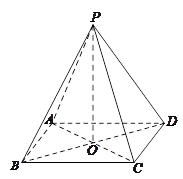
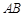
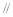 平面
平面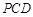 ;
;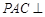 平面
平面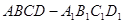 中,
中,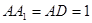 ,
,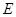 为
为 的中点,
的中点,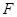 为
为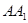 的中点.
的中点.
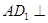 平面
平面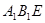 ;
;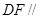 平面
平面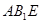 ;
;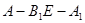 的大小为
的大小为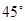 ,求
,求 的长.
的长.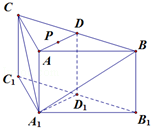
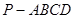 的侧面积为
的侧面积为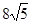 ,若
,若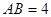 .
.
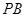 与平面
与平面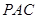 所成角的大小.
所成角的大小.