题目内容
【题目】在平面直角坐标系中,已知点P(3,0)在圆C:(x﹣m)2+(y﹣2)2=40内,动直线过点P且交圆C于A、B两点,若△ABC的面积的最大值是20,则实数m的取值范围是( )
A.(﹣3,﹣1]∪[7,9)
B.[﹣3,﹣1]∪[7,9)
C.[7,9)
D.(﹣3,﹣1]
【答案】A
【解析】解:圆C:(x﹣m)2+(y﹣2)2=40,圆心C(m,2),半径r=2 ![]() ,
,
S△ABC= ![]() r2sin∠ACB=20sin∠ACB,
r2sin∠ACB=20sin∠ACB,
∴当∠ACB=90时S取最大值20,
此时△ABC为等腰直角三角形,AB= ![]() r=4
r=4 ![]() ,
,
则C到AB距离=2 ![]() ,
,
∴2 ![]() ≤PC<2
≤PC<2 ![]() ,即2
,即2 ![]() ≤
≤ ![]() <2
<2 ![]() ,
,
∴20≤(m﹣3)2+4<40,即16≤(m﹣3)2<36,
∵圆C:(x﹣m)2+(y﹣2)2=40内,
∴|OP|= ![]()
![]() ,即(m﹣3)2<36,
,即(m﹣3)2<36,
∴16≤(m﹣3)2<36,
∴﹣3<m≤﹣1或7≤m<9,
故选:A.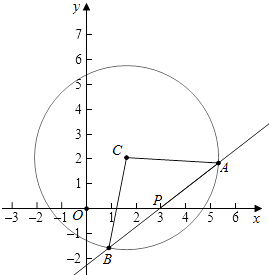

练习册系列答案
相关题目
